Consider the example below for minimum phase system. Write a code in MATLAB for the example given to reproduce the same figures as shown.

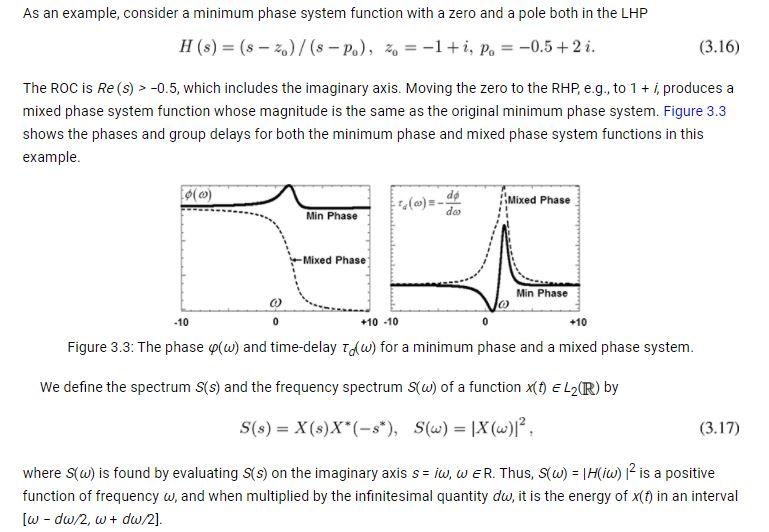
As an example, consider a minimum phase system function with a zero and a pole both in the LHP H(s) = (s - 2.)/(s - p.), z = -1+i, P. = -0.5+2i. (3.16) The ROC is Re (s) > -0.5, which includes the imaginary axis. Moving the zero to the RHP, e.g., to 1 + i produces a mixed phase system function whose magnitude is the same as the original minimum phase system. Figure 3.3 shows the phases and group delays for both the minimum phase and mixed phase system functions in this example. (6) Mixed Phase dos Min Phase -Mixed Phase Min Phase -10 0 +10 -10 +10 Figure 3.3: The phase (w) and time-delay Tdw) for a minimum phase and a mixed phase system. We define the spectrum S(s) and the frequency spectrum s(w) of a function X(t) EL2(R) by S(s) = X(s)X*(-s*), Sw) = X(w)!?. (3.17) where (w) is found by evaluating s(s) on the imaginary axis s= iW, W ER. Thus, S(W) = | H(w) is a positive function of frequency w, and when multiplied by the infinitesimal quantity dw, it is the energy of x(t) in an interval [w - dw/2, w+ dw/2]. As an example, consider a minimum phase system function with a zero and a pole both in the LHP H(s) = (s - 2.)/(s - p.), z = -1+i, P. = -0.5+2i. (3.16) The ROC is Re (s) > -0.5, which includes the imaginary axis. Moving the zero to the RHP, e.g., to 1 + i produces a mixed phase system function whose magnitude is the same as the original minimum phase system. Figure 3.3 shows the phases and group delays for both the minimum phase and mixed phase system functions in this example. (6) Mixed Phase dos Min Phase -Mixed Phase Min Phase -10 0 +10 -10 +10 Figure 3.3: The phase (w) and time-delay Tdw) for a minimum phase and a mixed phase system. We define the spectrum S(s) and the frequency spectrum s(w) of a function X(t) EL2(R) by S(s) = X(s)X*(-s*), Sw) = X(w)!?. (3.17) where (w) is found by evaluating s(s) on the imaginary axis s= iW, W ER. Thus, S(W) = | H(w) is a positive function of frequency w, and when multiplied by the infinitesimal quantity dw, it is the energy of x(t) in an interval [w - dw/2, w+ dw/2]