Question: Consider the following directed graph G(V,E): e1 V2 e4 V3 V1 e5 e3 e6 e2 e7 V4 V5 (i) Find the adjacency matrix A

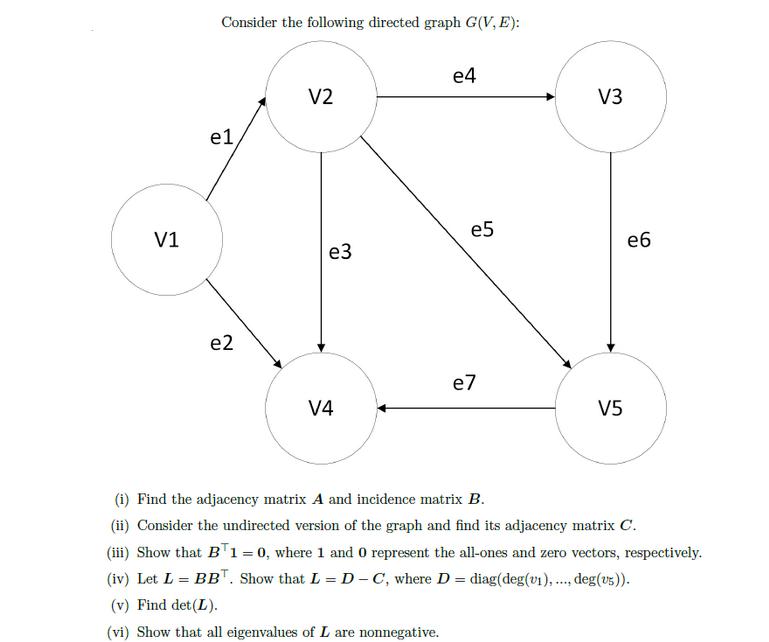
Consider the following directed graph G(V,E): e1 V2 e4 V3 V1 e5

Consider the following directed graph G(V,E): e1 V2 e4 V3 V1 e5 e3 e6 e2 e7 V4 V5 (i) Find the adjacency matrix A and incidence matrix B. (ii) Consider the undirected version of the graph and find its adjacency matrix C. (iii) Show that BT1 = 0, where 1 and 0 represent the all-ones and zero vectors, respectively. (iv) Let L = BBT. Show that L = D-C, where D = diag(deg(v1), ..., deg(vs)). (v) Find det(L). (vi) Show that all eigenvalues of L are nonnegative.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Case Study Questions - Mary Kay (Mary Kay Cosmetics: Sales Force Incentives - Harvard Business School) Please provide detail to the below questions from the Case Study. 1. Was MK A successful...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

The Excel file "table 8-6" presents information of 64 countries. The data has the following variables: CM = child mortality (number of deaths of children under age 5 in a year per 1000 live births)....

Delivery Service purchased a commercial umbrella policy with a $10 million liability limit and a $100,000 self-insured retention. The umbrella insurer required Delivery Service to carry a $1 million...

Given M in Problem, find M-1 and show that M-1M = 1. 102 011 121

8.3 Does a cash flow statement serve any useful purpose?

Tell me what you know about our organization and the position.

Present Value and Future Value Brian Inc. estimates that it will need $150,000 in ten years to expand its manufacturing facilities. A bank has agreed to pay Brian 5% interest compounded annually if...

Presented below are the financial statements of Swifty Corporation. Swifty Corporation Comparative Balance Sheets December 31 Assets 2022 2021 Cash $ 28,000 $ 16,000 Accounts receivable 16,000 11,200...

Summarize the percentage-of-sales technique used to forecast the required assets short-term liabilities in the Projected Balance Sheets

Breach of contract action by Opinion Survey Co. (P) against D, an unsuccessful presidential candidate. P claims that D failed to pay a large bill for political polling P had performed. D claims that...

Pre Pour Inspections include: Group of answer choices B. Rebar- material type, size, spacing, tie down, clearances C. Anchor Bolts- Projection, dimensionally square, nut on bottom secured, proper...

Alyssa launched her new shaver as being revolutionary, innovative, and unisex. Instead her brand is being purported as very feminine and too close to the Schick Shaver. What should Alyssa start to do?

A roofer is working to cover a 2,500squarefoot roof. He must first install rafters, then sheathing, then felt, and finally shingles. He assumes the previous tasks compose 35%, 20%, 15%, and 30% of...

Dakota is an unmarried taxpayer with one dependent child, age 18, living in Dakota's home. Dakota does not itemize deductions and reports AGI of $40,200. The dependent child earned $16,400 from a...

Hi-Tek Manufacturing, Incorporated, makes two types of industrial component parts-the B300 and the T500. An absorption costing income statement for the most recent period is shown: Hi-Tek...

Giant Company has just issued preferred stock with a par value of $100 and an annual dividend rate of 8.93 %. If your required rate of return is 12.89%, how much will you be willing to pay for one...

Discuss whether responsible human resources management should apply different standards for the home company and suppliers, for developed countries and developing countries, and for large companies...

At the Forrester Manufacturing Company, one repair technician has been assigned the responsibility of maintaining three machines. For each machine, the probability distribution of the running time...

Consider the following problem. Maximize Z = 3x1 + 2x2, Subject to and x1 ¥ 0, x2 ¥ 0. 51 3s 27

Reconsider the assignment problem formulation of Option 2 for the Better Products Co. problem presented in Table 9.29. Suppose that the cost of having Plant 1 produce product 1 is reduced from 820 to...

The financial statements of M&S (GBR) are presented in Appendix A. The company's complete annual report, including the notes to the financial statements, is available online. Instructions Refer to...

Wong Ltd. issues HK$2,000,000 of 7% bonds due in 10 years with interest payable at year-end. The current market rate of interest for bonds of similar risk is 8%. What amount will Wong receive when it...

Kraft Enterprises owns the following assets at December 31, 2019. Cash in bank-savings account..............................68,000 Cash on...