Question: Consider the following formula. n-1 sin(x) dx = ~ sin - 1(x) cos(x) + sin? - 2(x) dx n n Use the formula to find

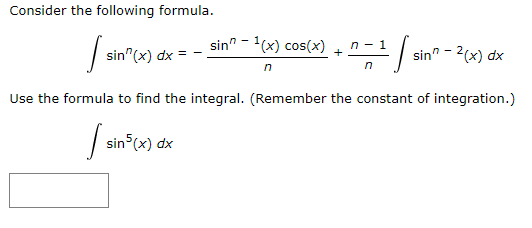
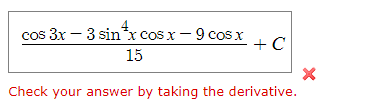
Consider the following formula. n-1 sin"(x) dx = ~ sin" - 1(x) cos(x) + sin? - 2(x) dx n n Use the formula to find the integral. (Remember the constant of integration.) sin (x) dxcos 3x - 3 sin x cos x - 9 cos x + C 15 Check your answer by taking the derivative.( sin x dex = - sin a loss + n -) in ( sin 2 - 2 ( sinsuda here me s ( sinsuda = - sini los 4( sin 3 x did 5 for ( sin bu due n2 3 Ssings dre = + 2 s sinn du 3 3 = - Sin u Cosa _ 2 los + C 3 3 -" ( sin Sudd = - sinn cosu sinzu cosu _ 2 Losud + C S 3 3 = - sincosu - 4sinbecos - 8 cos + C 5 IS 15 = - 3 sinn cost - 4 sinha cos - 8 costd C working everything interms of losings and simplifyry, we get Ssinsx du = - 1 cos v + 2 Cos'x - Cosm + C

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

I want ans asap cos 3x sin c 31. 32 (a2 + 1) 2 dx dx 2 + 4x + 5 " cos 2x 33. dx 34. x sin x dx 4 + 1 4 + 1 cos x 35. r sin x dx 36. (2 + 1) (x2 + 4)" dx (x2 + 1) (2 + 9) 37. sin x x ti . dx [Hint:...

Use integration by parts to derive the following formula x " . In / x / dx = x" + In x n+1 + Cin -1 (n + 1)- Find uv. uv = Integrate vdu vdu = After finding uv, integrating vdu, and subtracting vdu...

1 hour to answer, Please provide a complete solution. I will give a good feedback. Thank you. Integration by Substitution Use Integration by Substitution to find J sin(x2) 2x dx A sin(x-) + c B -...

Evaluate the definite integral below. K 7 1/6 IS sin x dx - It/2 7x/6 sin x dx = - It/ 2 (Type an exact answer.)Use the given information to solve the triangle shown in A the figure to the right. C a...

verify that the indicated function is an explicit solution of the given differential y" + y = tan x; y = (cos x)ln(secx + tan .x) Question 2: verify that the indicated family of functions is a...

Use the reduction formula integral (b)use part (a) to evaluate the following. (c) Use part (a) to determine which of the following is correct for odd powers of sine. 1 cos x sin" n - 1 sin" x dx = -...

Consider the Deer-Moose model whose vector field and trajectories are shown below. This model has four equilibrium points shown by the black dots. Explain in words what the basins of attraction of...

7/4/23, 11:16 PM Homework 8.7-Anh Nguyen Use a table of integrals to determine tv7t+ 19 at. Click here to view page 1 of the integral table. " Click here to view page 2 of the integral table. 14...

1. Evaluate the following integrals. ( a) VI - x - dx. (S.R: u = V1 -x.) (b) / (Inx)'dx. (IBP) Answer: x((Inx)3 - 3(Inx)2 + 6Inx -6) + C (c) xledx. (S.R + IBP) Answer: (20-De + C (d) tan'x secada....

please use this format filename 1 .. 10 name file 2 1 .. 10 Back Indefinite Integrals Graded Quiz - 30 min - 10 total points Due Sep 25, 11:59 PM WIB True or false? If the function f is continuous on...

In our Nodhead example, true depreciation was decelerated. That is not always the case. For instance, figure shows how on average the value of a Boeing 737 has varied with its age. 28 Table 12.11...

What does current pension accounting (SFAS158) recognize in the balance sheet? How is it different from what was recognized earlier (under SFAS 87)?

BE3.4 (LO 2, 3) The following information is provided. Sales revenue HK$100,000 Gain on sale of plant assets 30,000 Selling and administrative expenses 10,000 Cost of goods sold 55,000 Interest...

1 3 . A comparative adA ) reinforces previous knowledge of a product.B ) assures current users they made the right choice.C ) promotes a specific brand's features and benefits.D ) tells people what a...