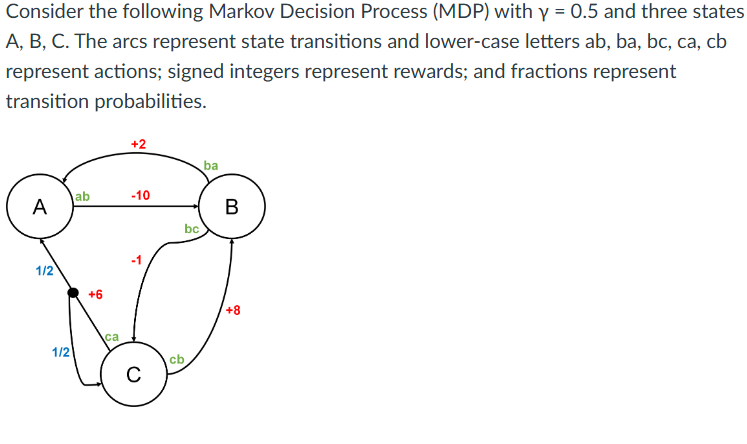
Consider the following Markov Decision Process $($MDP$)$ with $=0\mathrm{.}5$ and three states A$,$ B$,$ C$.$ The arcs represent state transitions and lower$-$case letters ab$,$ ba$,$ bc$,$ ca$,$ cb represent actions; signed integers represent rewards; and fractions represent transition probabilities.

$$

$1.(1\%)$ Write down the Bellman expectation equation for state$-$value functions

$$

$$

$$

$2.(3\%)$ Consider the uniform random policy $1($s$,$a$)$ that takes all actions from state s with equal probability. Starting with an initial value function of V$1($A$)=$V$1($B$)=$V$1($C$)=4,$ apply one synchronous iteration of iterative policy evaluation $($i$.$e$.$ one backup for each state$)$ to compute a new value function V$2($s$)($i$.$e$.,$ V$2($A$),$ V$2($B$),$ and V$2($C$))$ by applying$/$expanding the equation given in part $1.$

$$

$$

$$

$3.(1\%)$ Write the Bellman function that characterizes the optimal state value function $($i$.$e$.,$ V$*($s$))$ Consider the following Markov Decision Process $($MDP$)$ with $\backslash (\backslash$gamma$=0\mathrm{.}5\backslash )$ and three states A$,$ B$,$ C$.$ The arcs represent state transitions and lower$-$case letters ab$,$ ba$,$ bc$,$ ca$,$ cb represent actions; signed integers represent rewards; and fractions represent transition probabilities.