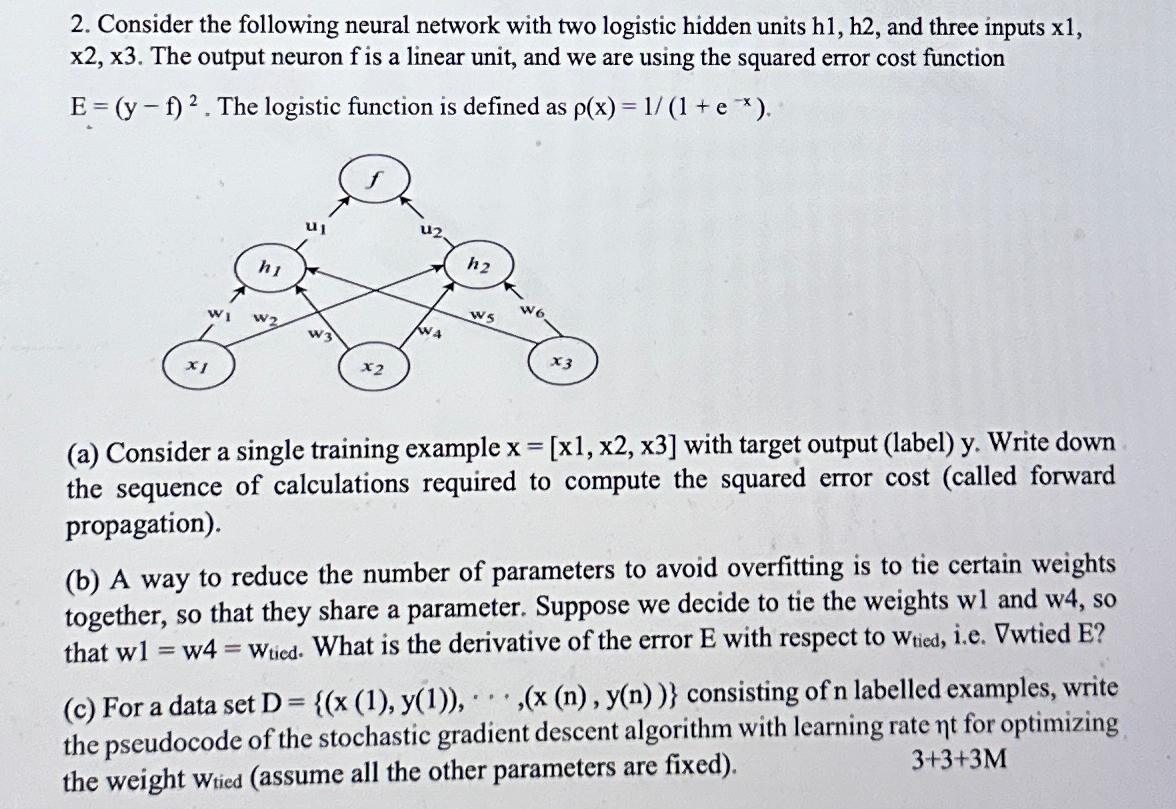
Consider the following neural network with two logistic hidden units $h1,h2,$ and three inputs $x1,x2,x3.$ The output neuron $f$ is a linear unit, and we are using the squared error cost function $E=(y-f{)}^2.$ The logistic function is defined as $(x)=\frac{1}{1+e^{-x}}.$

$($a$)$ Consider a single training example $x=[x1,x2,x3]$ with target output $($label$)y.$ Write down the sequence of calculations required to compute the squared error cost $($called forward propagation$).$

$($b$)$ A way to reduce the number of parameters to avoid overfitting is to tie certain weights together, so that they share a parameter. Suppose we decide to tie the weights wl and w$4,$ so that $w1=w4=w_{\text{t}\text{i}\text{e}\text{d}}.$ What is the derivative of the error $E$ with respect to $w_{\text{t}\text{i}\text{e}\text{d}},$ i$.$e$.$ Dwtied E$?$

$($c$)$ For a data set $D=\{(x(1),y(1)),$cdots,$(x(n),y(n))\}$ consisting of $n$ labelled examples, write the pseudocode of the stochastic gradient descent algorithm with learning rate $t$ for optimizing the weight wtied $($assume all the other parameters are fixed$).$

$3+3+3M$

PLEASE WRITE THE COMPLETE CALCULATED SOLUTION ONLY