Question: Consider the weighted graph below. G 5 H 1 3 6 th 5 5 00 6 D F 00 8 2 6 3 8 5

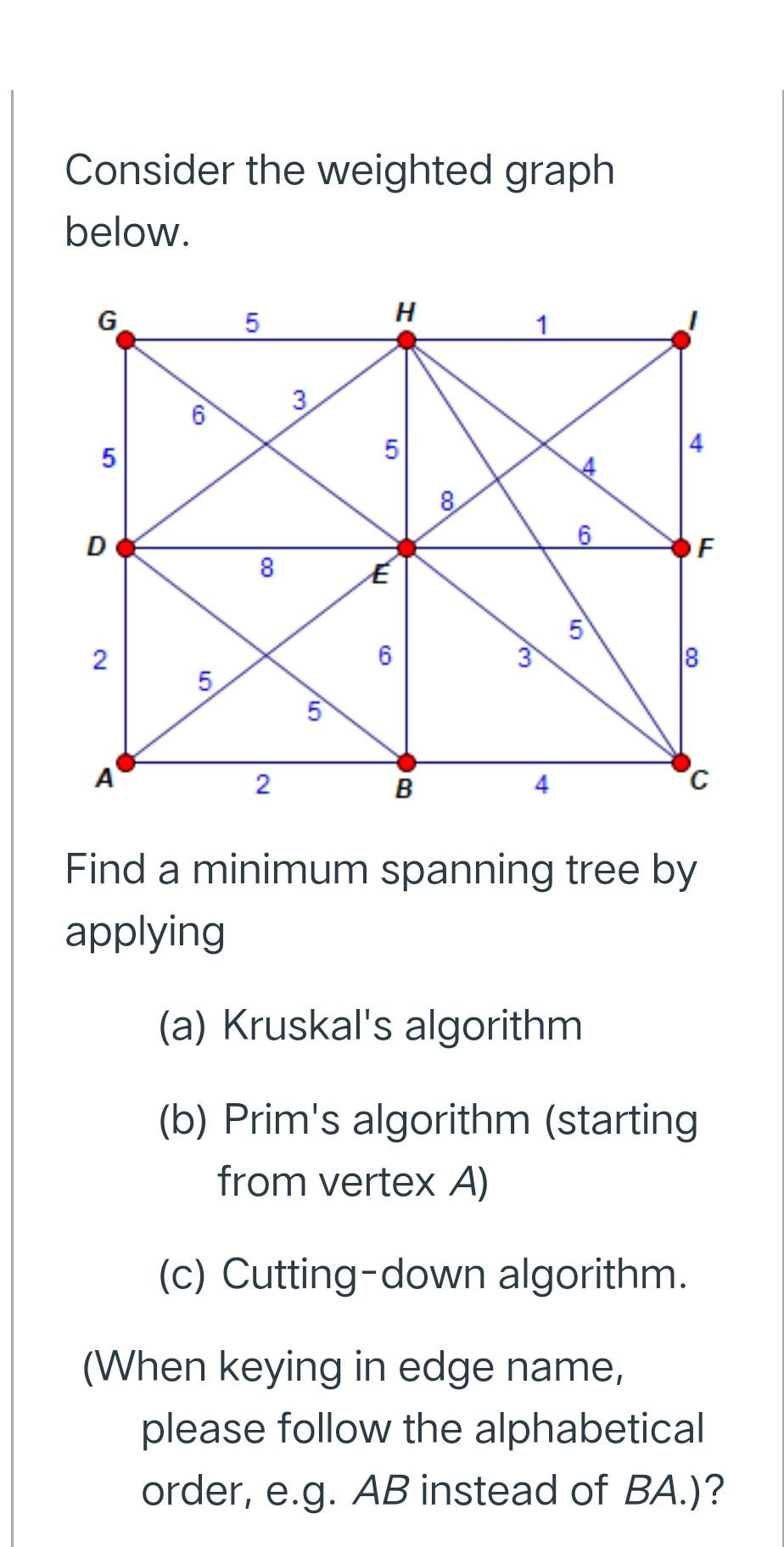
Consider the weighted graph below. G 5 H 1 3 6

th 5 5 00 6 D F 00 8 2 6 3

8 5 5 A 2 B C Find a minimum spanning tree

by applying (a) Kruskal's algorithm (b) Prim's algorithm (starting from vertex A)

Consider the weighted graph below. G 5 H 1 3 6 th 5 5 00 6 D F 00 8 2 6 3 8 5 5 A 2 B C Find a minimum spanning tree by applying (a) Kruskal's algorithm (b) Prim's algorithm (starting from vertex A) (c) Cutting-down algorithm. (When keying in edge name, please follow the alphabetical order, e.g. AB instead of BA.)? (a) In the execution of Kruskal's algorithm, What is the third edge added to the spanning tree? What is the weight of the sixth edge added to the spanning tree? (b) In the execution of Prim's algorithm (starting from vertex A), What is the third edge added to the spanning tree? What is the weight of the fifth edge added to the spanning tree? What is the weight of the fifth edge removed from the graph? What is the last edge removed from the graph? What is the weight of a minimum spanning tree? How many minimum spanning trees are there

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Answer questions 1-8 using the excel. A B 1 WEIGHTED AVERAGE 2 PROCESS COST 3 ******* 4 A B Data Section: Work in process, beginning Units completed during month Work in process, ending Costs to...

D I E GradesforRik X I M InbOXerikkiluv X I @ p385790.pdf X I @ ARZUOeLpdf X a USAJOBSeJot X rcraeYahoo 55 X I fgsenvironme X I + 7 j X 6 9 G [5 https://www.usajobs.gov/job/725009600# 1:. [:3 A\" [R...

using c++ create a function to read in and display a graph using coordinates below [0, 0]-41 [0, 1]-93 [0, 2]-90 [0, 3]-24 [0, 4]-70 [0, 5]-39 [0, 6]-47 [0, 7]-35 [0, 8]-83 [1, 0]-38 [1, 1]-66 [1,...

Cour An annuity pays $11 per year for 53 years. What is the future value (FV) of this annuity at the end of that 53 years given that the discount rate is 5%? Purch O A $3.240.59 OB. $1,620 29 OC....

Which molecule has given rise to the spectra shown below. Justify your answer with respect to IR, 1 H NMR and 13 C NMR. Keep in mind that Hs that switch with D2O usually do not show connections to...

answers in excel formulas please 5. Using the SML- Excel 6 ? ES X FILE HOME INSERT PAGE LAYOUT FORMULAS DATA REVIEW VIEW Sign In Arial 12 M Paste BIU- 5 nts = % Alignment Number Conditional Format as...

What is the network slack time assuming the customer satisfaction calls for the project to be completed in 21days? Cal. The slack time for all events not on the critical path Activity Initial Node...

3. Given the following network with activities and times estimated in days, D A Start B F K Finish c Most Activity Optimistic Probable A 2 5 B 1 3 6 7 D 5 12 E 3 4 F 8 9 G 4 6 H 3 6 5 7 12 13 K 1 3...

CASE STUDY [30 Marks] A computer network company installs network points. The project manager has been very concerned with the amount of time it took to complete several recent jobs. The data...

Given the following product structure diagram for A: . B (2) (3) D (3) E (3) F (2) G (5) H (2) (3) 1. How many E's are needed to make 900 A's? Be sure to include the entire diagram. E (5) J (5) Given...

Five years ago, when the relevant cost index was 120, a nuclear centrifuge cost $40,000. The centrifuge had a capacity of separating 1500 gallons of ionized solution per hour. Today, it is desired to...

An equation for potential energy states U = mgh. If U is in joules, with m in kg, h in m, and g in m/s2 find the combination of SI base units that are equivalent to joules.

answer this 11. In the histogram below, which of the following values of b; would be considered "unlikely"? 0 O WD > by = 2.5 by = 5.2 by = 2.5 b =0 middle(b1, 0.95) FALSE TRUE

P7-2 (LO3) GROUPWORK (Bad-Debt Reporting) The following are a series of unrelated situations. 1. Halen Company's unadjusted trial balance at December 31, 2017, included the following accounts. Debit...

2. What are your challenges in the creative process?

___ 28. I am most fulfilled in my work when I feel that I have complete financial and employment security.

___ 29. I will feel successful in my career only if I have succeeded in creating or building something that is entirely my own?