Could I please get the worked solution for the following question:

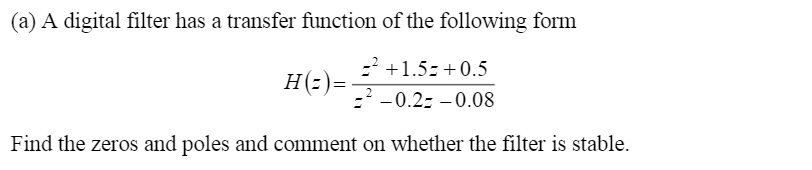
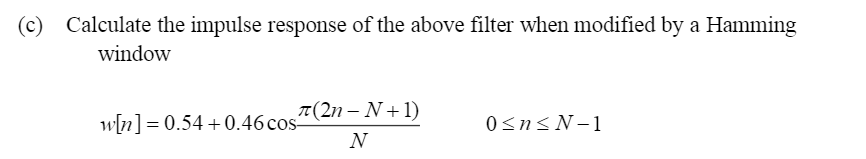
(a) A digital filter has a transfer function of the following form H(z)=z20.2z0.08z2+1.5z+0.5 Find the zeros and poles and comment on whether the filter is stable. Determine the impulse response of a non-recursive digital filter using an N=8 inverse discrete Fourier transform (IDFT) sequence based on a filter frequency response of H[k]=[1.0,0.5,0,0,0,0,0,0.5. You may use the definition of the inverse discrete Fourier transform x[n]=N1k=0N1X[k]ejN2kn, and for W8=ej82, W80=1,W81=0.707+0.707j,W82=j,W83=0.707+0.707j,W84=1,W85=0.7070.707j,W86=j,W87=0.7070.707j. (c) Calculate the impulse response of the above filter when modified by a Hamming window w[n]=0.54+0.46cosN(2nN+1)0nN1