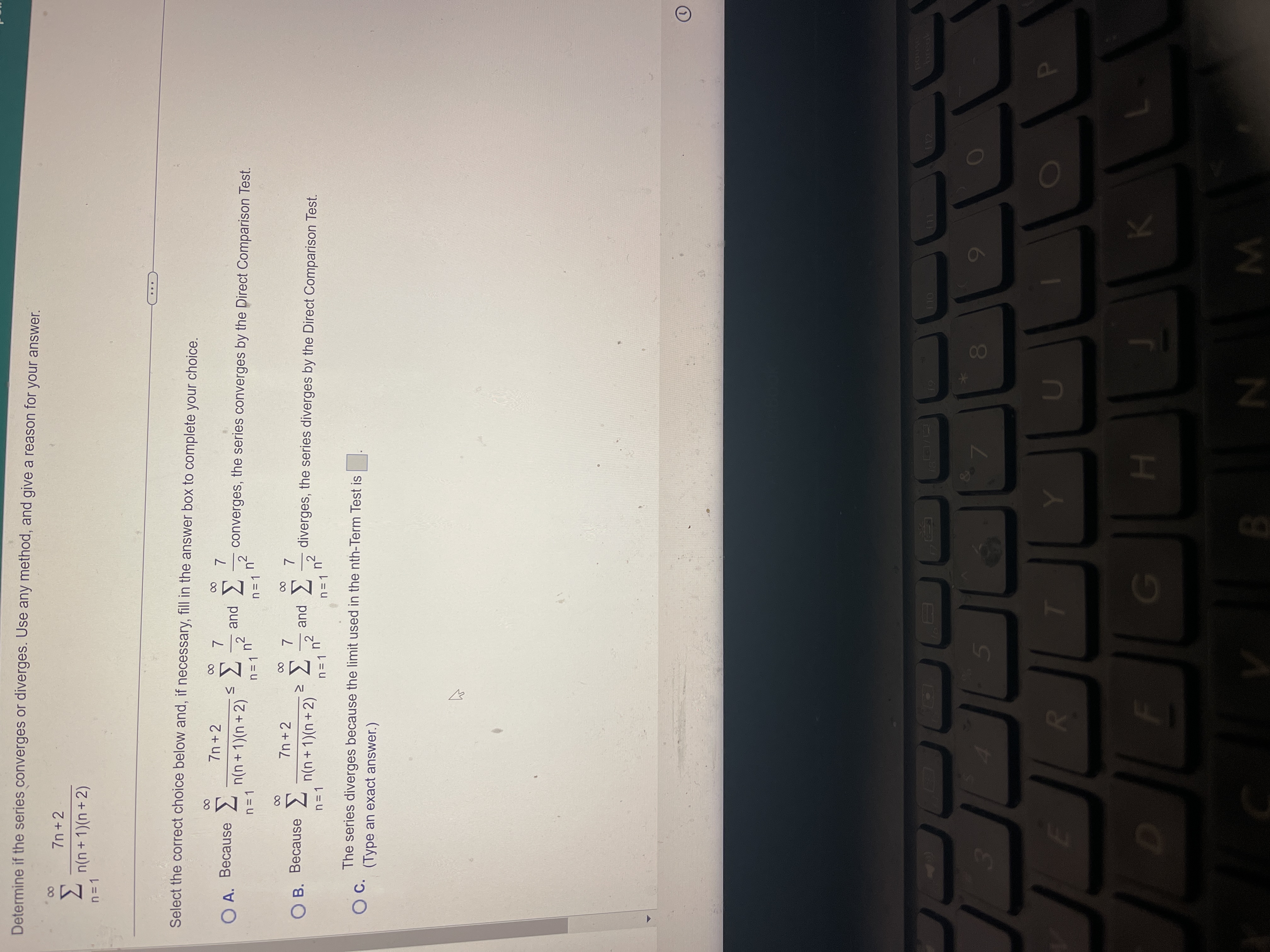
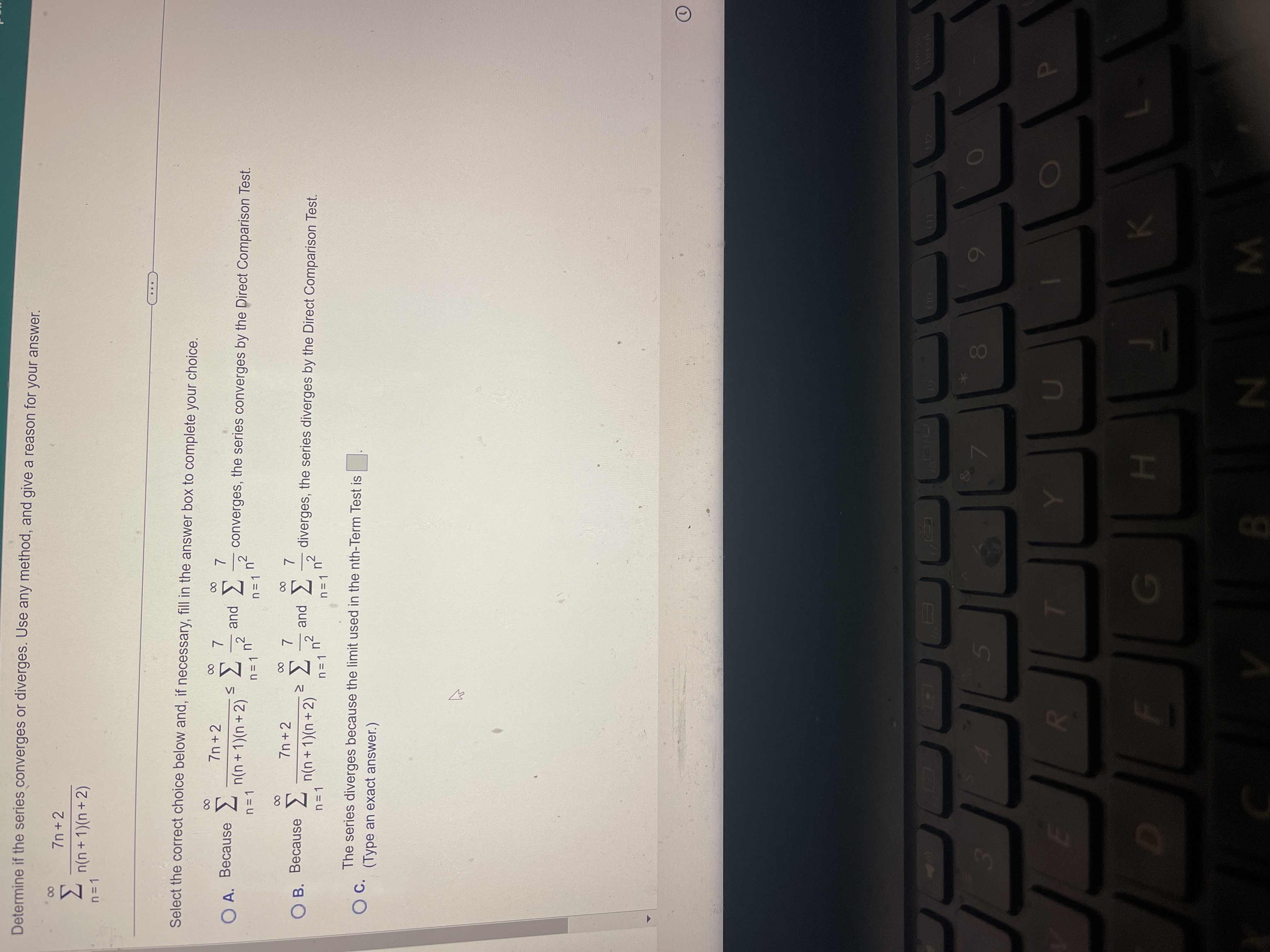
Determine if the series converges or diverges. Use any method, and give a reason for your answer. 7n + 2 n = 1 n(n + 1)(n+ 2) Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. Because 7n + 2 7 and n = 1 n(n + 1)(n+2) n= 1 h n= 1n converges, the series converges by the Direct Comparison Test. O B. Because 7n + 2 00 and - n = 1 n (n + 1)(n+2) n = 1 n n= 1 n diverges, the series diverges by the Direct Comparison Test. O C. The series diverges because the limit used in the nth-Term Test is (Type an exact answer.) 5 8 R P H K