Draw a truth table for a system with 3 inputs, a, b, c, and d and one output, f.

f is 1 iff n is a prime

f is 0 iff n is not a prime

Note that, 0 and 1 are not primes. Prime numbers are 2, 3, 5, and 7

Reduce the expression below (using switching algebra) to a sum of products expression with 2 terms and 4 literals. Show each step.

a' b' c' + a' b' c + a b c + a b' c

Draw a block diagram for the reduced expression.

Consider the following truth table

x	y	z	F
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

a) Write a canonical SOP (sum of minterms function) in numeric form.

f(x,y,z) = m( 0,

b) Write a sum of minterms function in algebraic form.

f(x,y,z) = x' yz + ...

c) Find a minimum sum of products expression.

d) Write a canonical POS (sum of maxterms function) in numeric form.

f(x,y,z) = M (1, ...

e) Write a sum of maxterms function in algebraic form (for example,

f(x,y,z) = (x + y + z) . ...

For the following function, find a minimum sum of products expression using K-map.

f (a, b, c, d) = m (2, 4, 5, 9, 11, 12, 13)

For the following function, find BOTH minimum sum of products expressions. (A blank map is given for your convenience.).

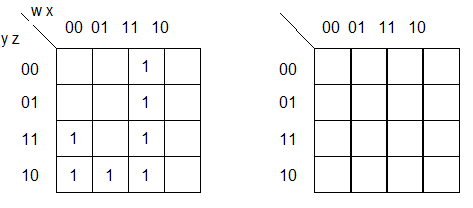
Which prime implicants are not essential?