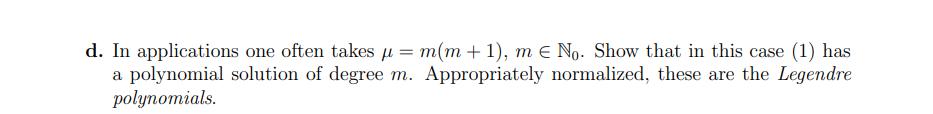
Exercise 9. Consider Legendre's differential equation (1-x)y" - 2xy + y = 0, -1 < x < 1. a. Show that a = 0 is an ordinary point of (1). (1) b. Give a lower bound on the radius of convergence of the power series solutions to (1) of the form - Cana". n=0 y = c. Find the recursion relation satisfied by the coefficients an of the solutions y of part b. d. In applications one often takes = m(m + 1), m E No. Show that in this case (1) has a polynomial solution of degree m. Appropriately normalized, these are the Legendre polynomials.