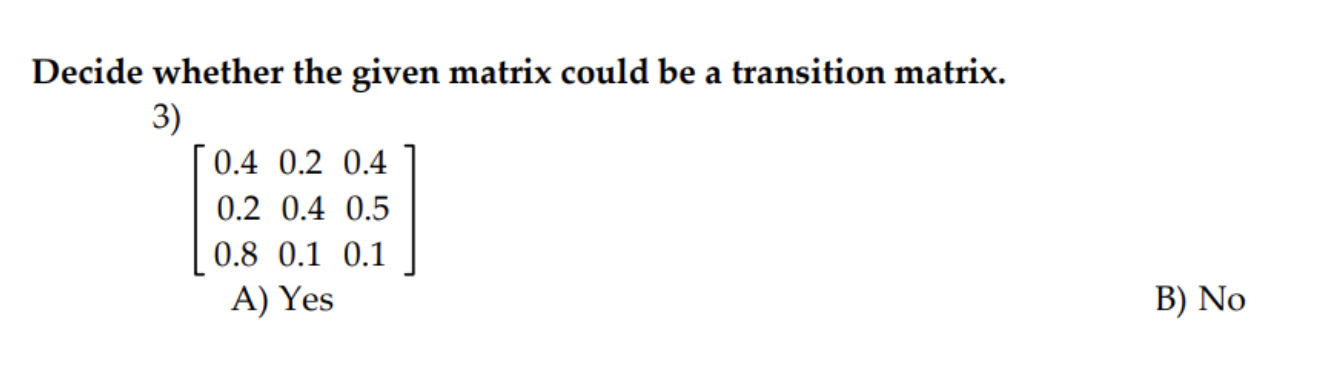
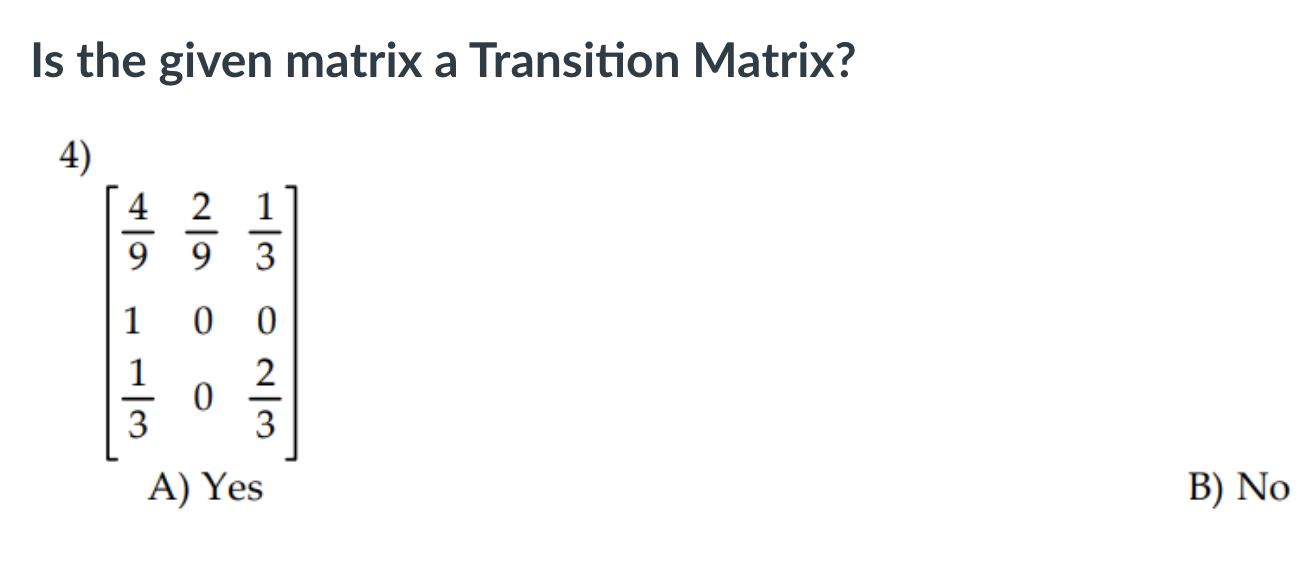
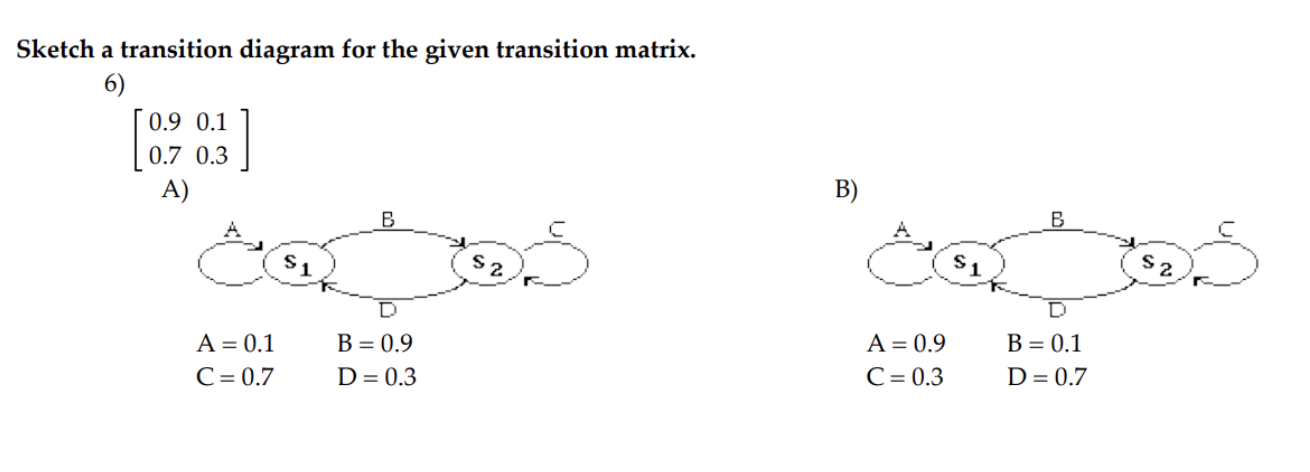
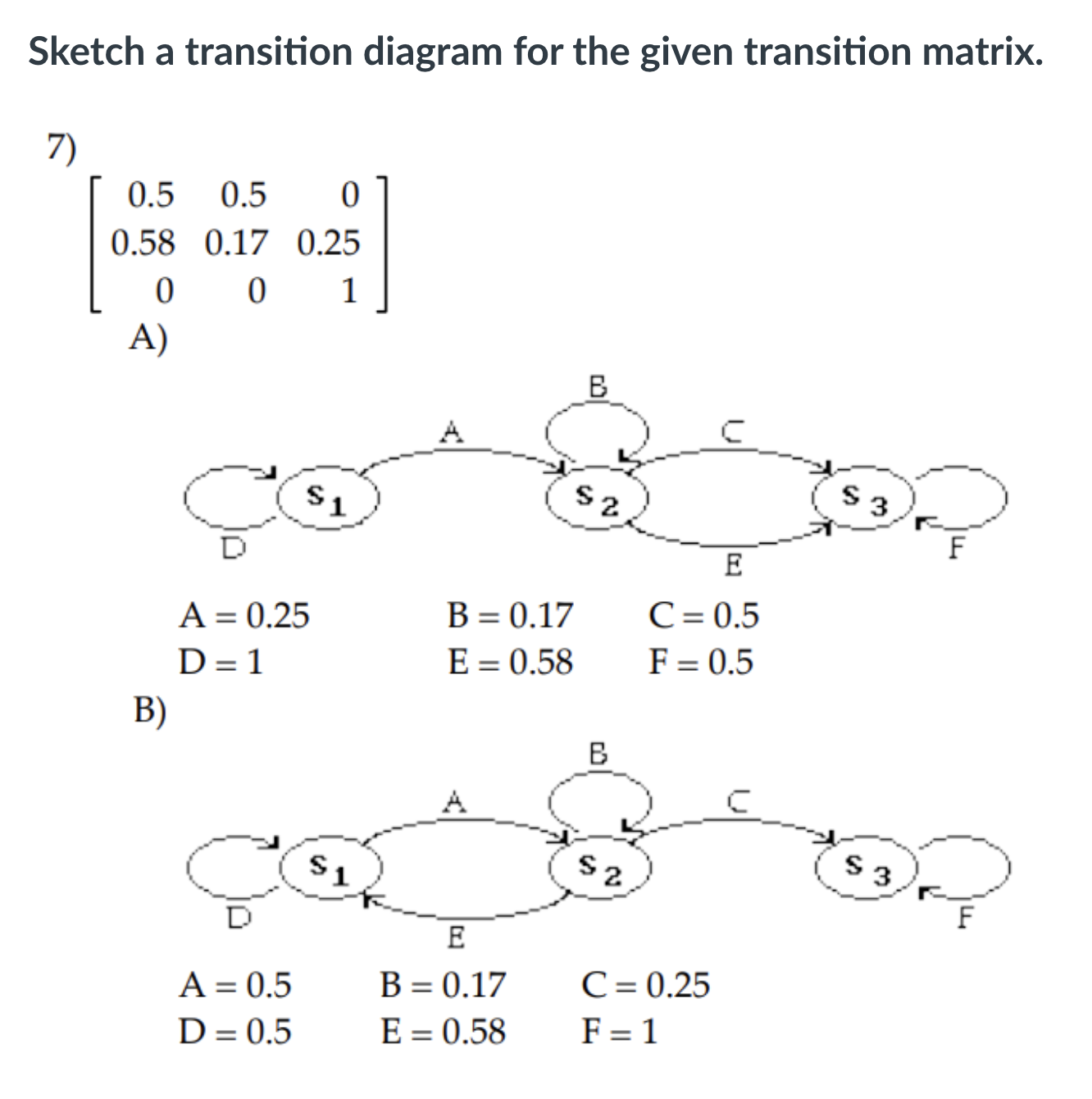
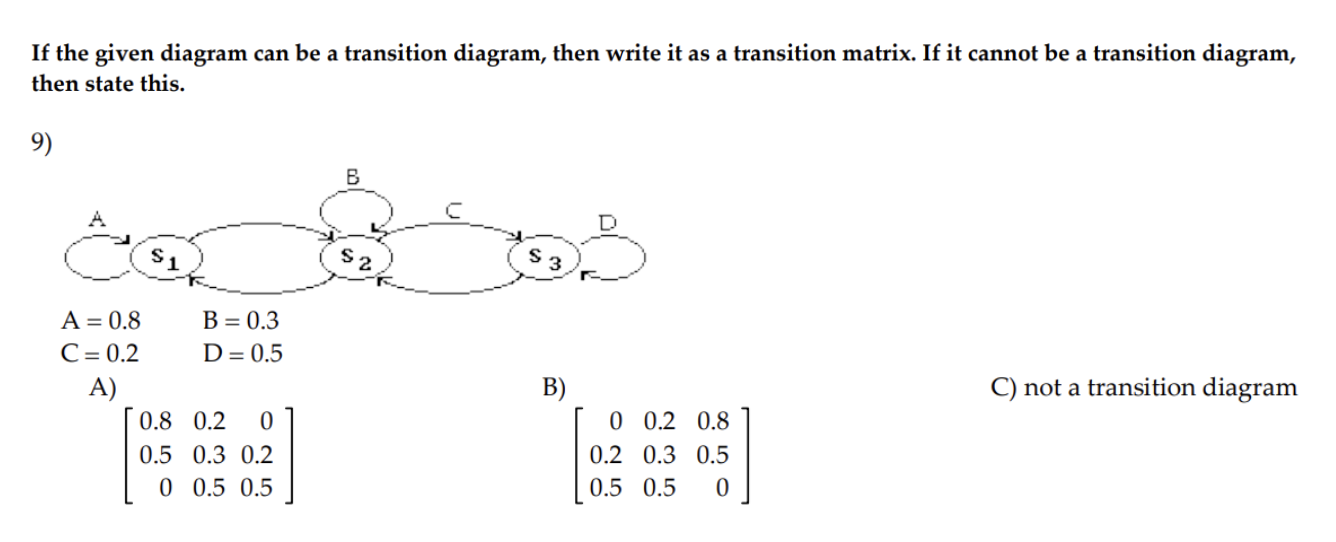
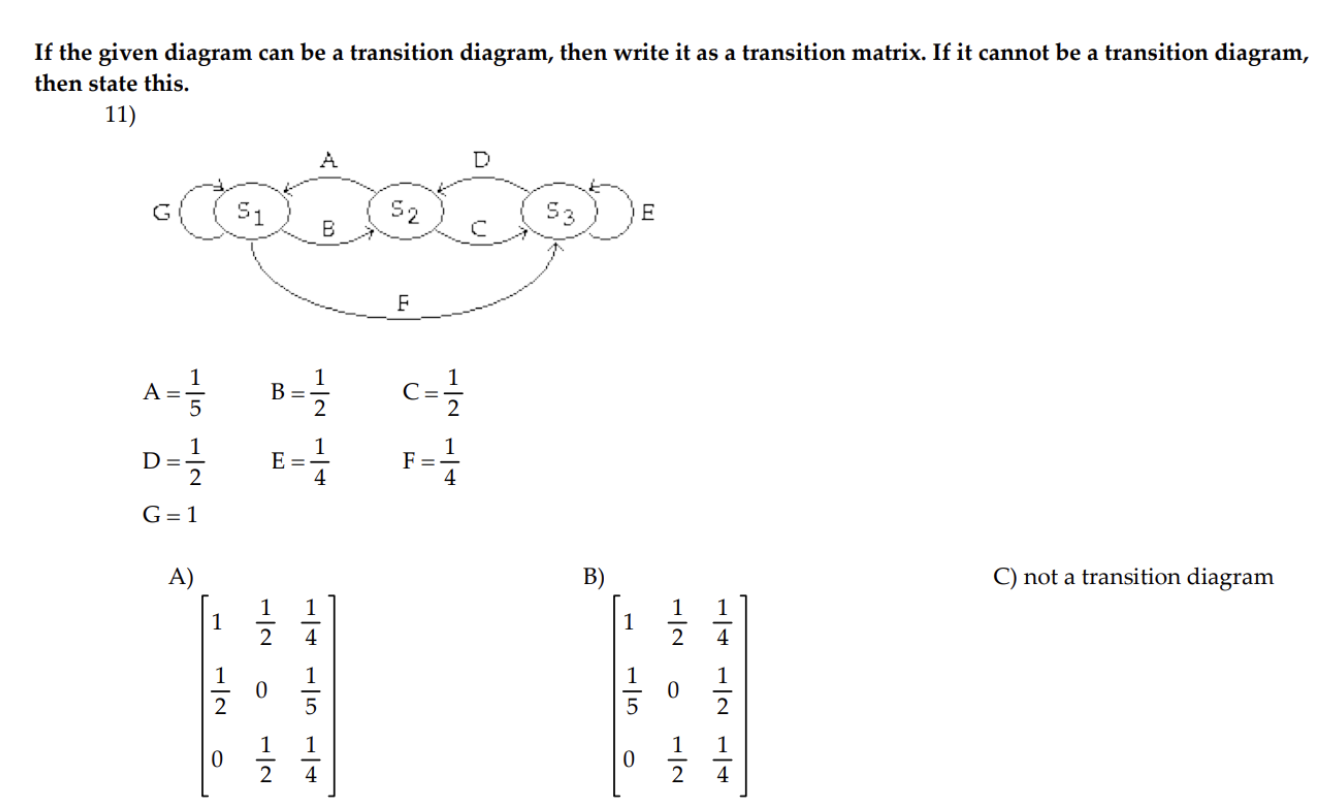
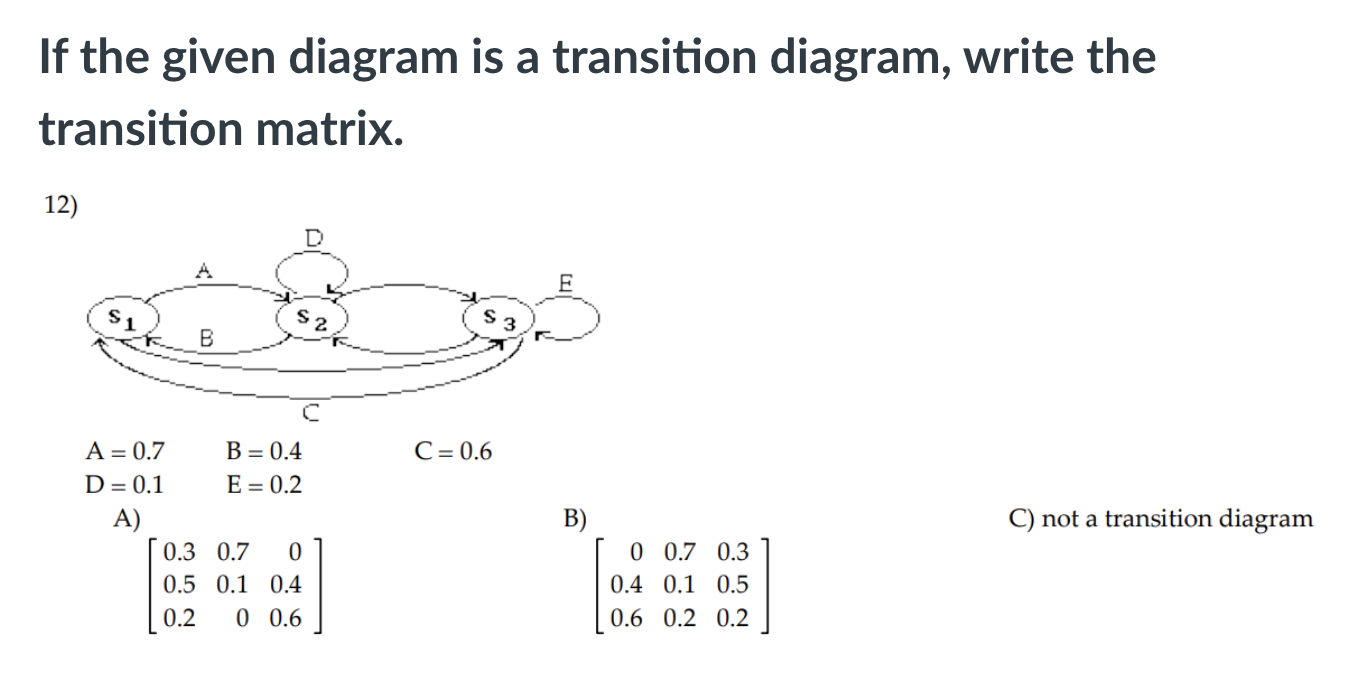
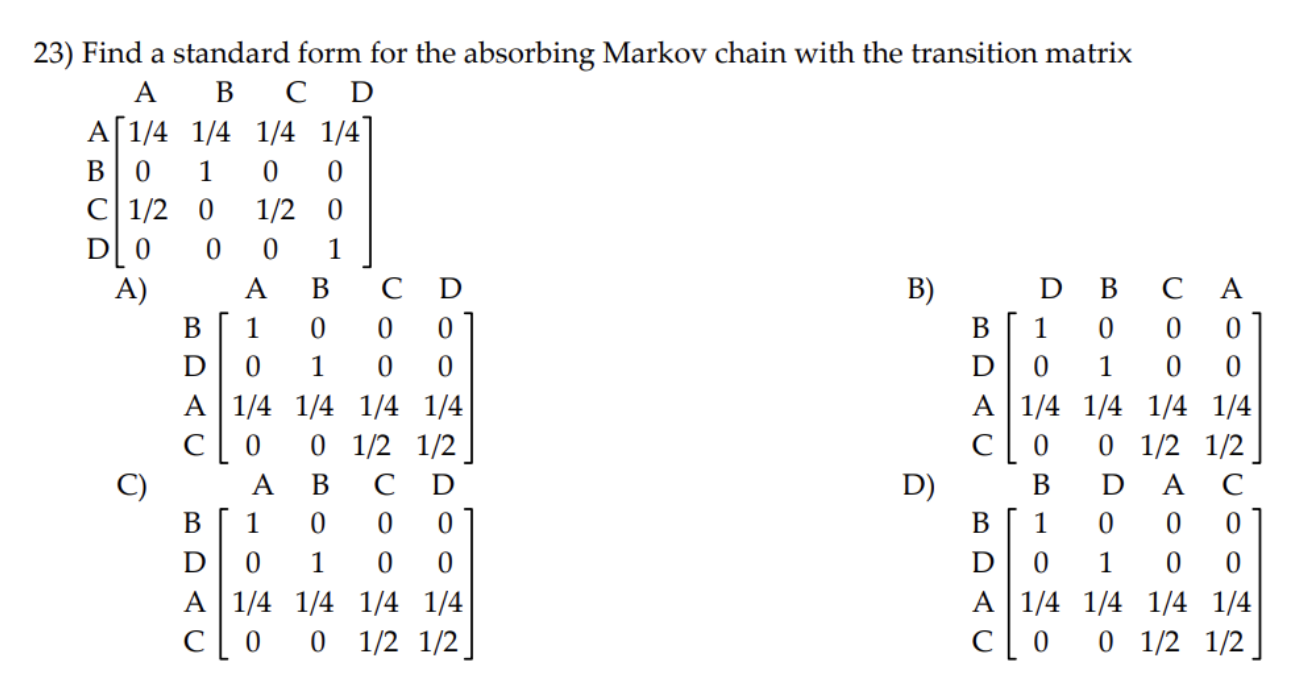
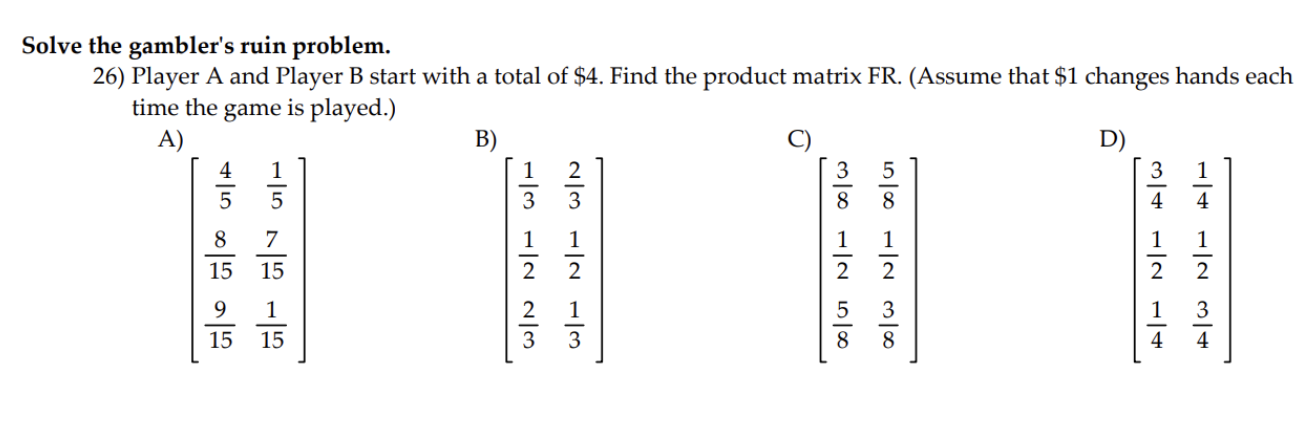
\fDecide whether the given matrix could be a transition matrix. 3) 0.4 0.2 0.4 0.2 0.4 0.5 0.8 0.1 0.1 A) Yes B) No \fFor the given transition matrix, find the probability that state 2 changes to state 1 after three repetitions of the experiment. 0.4 0.3 0.3 5) A = 0 0 1 0.7 0.1 0.2 A) 0.41 B) 0.30 C) 0.35 D) 0.42 \f\fIf the given diagram can be a transition diagram, then write it as a transition matrix. If it cannot be a transition diagram, then state this. 8) 0.4 S 2 0.9 A) B C) not a transition diagram 0.9 0.1 0.6 0.4 0.4 0.6 0.1 0.9If the given diagram can be a transition diagram, then write it as a transition matrix. If it cannot be a transition diagram, then state this. 9) B C 1 $ 2 S 3 A = 0.8 B = 0.3 C =0.2 D = 0.5 A) B) C) not a transition diagram 0.8 0.2 0 0 0.2 0.8 0.5 0.3 0.2 0.2 0.3 0.5 0 0.5 0.5 0.5 0.5 0Construct the transition matrix that represents the data. 10) 10 percent of the people in one generation who have a certain physical characteristic will pass that characteristic on to the next generation. 40 percent of the people in one generation who do not have this characteristic will pass it on to the next generation. A) B) C) D) 0.1 0.9 0.4 0.6 0.9 0.1 0.6 0.4 0.4 0.6 0.1 0.9 0.6 0.4 0.9 0.1 If the given diagram can be a transition diagram, then write it as a transition matrix. If it cannot be a transition diagram, then state this. 11 ) A=% 3:; C=% 1):; E=i F=i G=1 A) B) C) not a transition diagram 1 a 1 %% so a go % o a o a; If the given diagram is a transition diagram, write the transition matrix. 12 ) A S S 2 3 B C A = 0.7 B = 0.4 C =0.6 D = 0.1 E = 0.2 A) B) C) not a transition diagram 0.3 0.7 0 0 0.7 0.3 0.5 0.1 0.4 0.4 0.1 0.5 0.2 0 0.6 0.6 0.2 0.213) The transition matrix for a Markov process is: State A B State A | 0.3 0.7 = P B 0.9 0.1] Find the first state matrix if the initial state is So = [.3 .7]. A) [0.3 0.7] B) [0.72 0.28] C) [0.9 0.1] D) [0.468 0.532]\f15) Given the transition matrix: A B c D A B C D A 0.4 0.3 0.2 0.1 A 0.0396 0.5942 0.3518 0.0144 P23 0 1 0 0 P4: B 0 1 0 0 C 0 0 1 0 C 0 0 1 0 D 0.2 0.5 0.1 0.2 D 0.0288 0.756 0.2044 0.0108 Find the probability of going from state A to state D in four trials. A) 0.3518 B) 0.0144 C) 0.0396 D) 0 17) Dublin is experiencing a population movement out of the city to the suburbs. Currently 85% of the total population live in the city with the remaining 15% living in the suburbs. It has been shown that each year 7% of the city residents move to the suburbs, while only 1% of the Suburb population move back to the city. Assuming population remains constant for both, what percent of the total will remain in the city after 2 years. Express your answer rounded to hundredths of a percent. A) 31.05% B) 73.86% C) 26.14% D) 79.2% Construct the transition matrix that represents the data. 18) A new antigravity commuter train has been installed. It is expected that each week 90% of the riders who used the existing system will continue to do 50. Of those who traveled by car, 5% will begin to use the new anti-gravity train. Use this information to write the transition matrix that describes this process. T C Ell A) T c B) T C C) T c D) T c T 0.95 0.10 T 0.90 0.05 T 0.90 0.10 T 0.95 0.10 c 0.05 0.90 c 0.10 0.95 c 0.05 0.95 c 0.05 0.95 Decide whether or not the transition matrix is regular. 19) 0.31 0 0.69 1 0 0 0 0510.49 A) Yes B) No 0.2 0.6 0.2 20) Find the stationary matrix for the transition matrix P = 0.1 0.1 0.8 0.3 0.3 0.4 10 0 5 7 11 23 23 23 A) [5 7 11] B) 010 C) 23 23 23 D) 5 7 1 0 0121) The probability that a car owner will become a car renter in ve years is 0.03. The probability that a renter will become an owner in ve years is 0.1. Suppose the proportions in the population are 64% owners (0), 35.5% renters (R) and 5% neither (N) with the following transition matrix. 0 R N O 0.94 0.06 0 R 0.12 0.879 0.001 N 0 32 0.68 Find the longrange probabilities for the three categories. A) [0.94 0.879 0.001] B) [0.666 0.333 0.001] C) [0.94 0.06 0] D) [0.64 0.355 0.005] 23) Find a standard form for the absorbing Markov chain with the transition matrix A B C D A 1/4 1/4 1/4 1/4 B O 1 O 0 C 1/2 0 1/2 0 D 0 0 0 1 A) A B C D B) D B C A B 1 0 0 0 B 1 0 0 0 D 0 1 0 0 D 0 1 0 0 A 1/4 1/4 1/4 1/4 A 1/4 1/4 1/4 1/4 C 0 0 1/2 1/2 C 0 0 1/2 1/2 C) A B C D D) B D A C B 1 0 0 0 B 1 0 0 0 D 0 1 0 0 D 0 1 0 0 A 1/4 1/4 1/4 1/4 A 1/4 1/4 1/4 1/4 C 0 0 1/2 1/2 C 0 0 1/2 1/2 24) Among first-year students enrolled in a two-year program at a trade school, the following was determined to be true: 73% would successfully complete the year and go on to the second year; 18% would repeat the year; and 9% would drop out of the program. Among the second -year students, 85% would successfully complete the year and graduate; 8% would repeat the year; and 7% would drop out of the program. In the long run, what percentage of the second-year students will drop out of the program? Round your answer to the nearest whole number. A) 17% B) 2% C) 8% D) 12% 25) There are five brands of a product on the market, three of which have very loyal customers who never change brands. The transition matrix for the five brands is shown below (where the brands are labeled A, B, C, D, and B). About how many times, on average, will a person currently using brand C use brand D before trying one of the brands that have loyal followings? Round your answer to the nearest hundredth. A B C D E A 1 0 0 0 0 B 0 1 0 0 O C 0.12 0.14 0.15 0.17 0.42 D 0.17 0.25 0.11 0.12 0.35 E 0 0 0 0 1 A)1.16 B) 1.21 C) 0.23 D) 0.15 Solve the gambler's ruin problem. 26) Player A and Player B start with a total of $4. Find the product matrix FR. (Assume that $1 changes hands each time the game is played.) C) D) A) B) A/ H N /H A/W 00 / W N / H 00 / 07 8 00 / UT N / H 00/ W W / H N / H W/ N W/ N N/H W/H