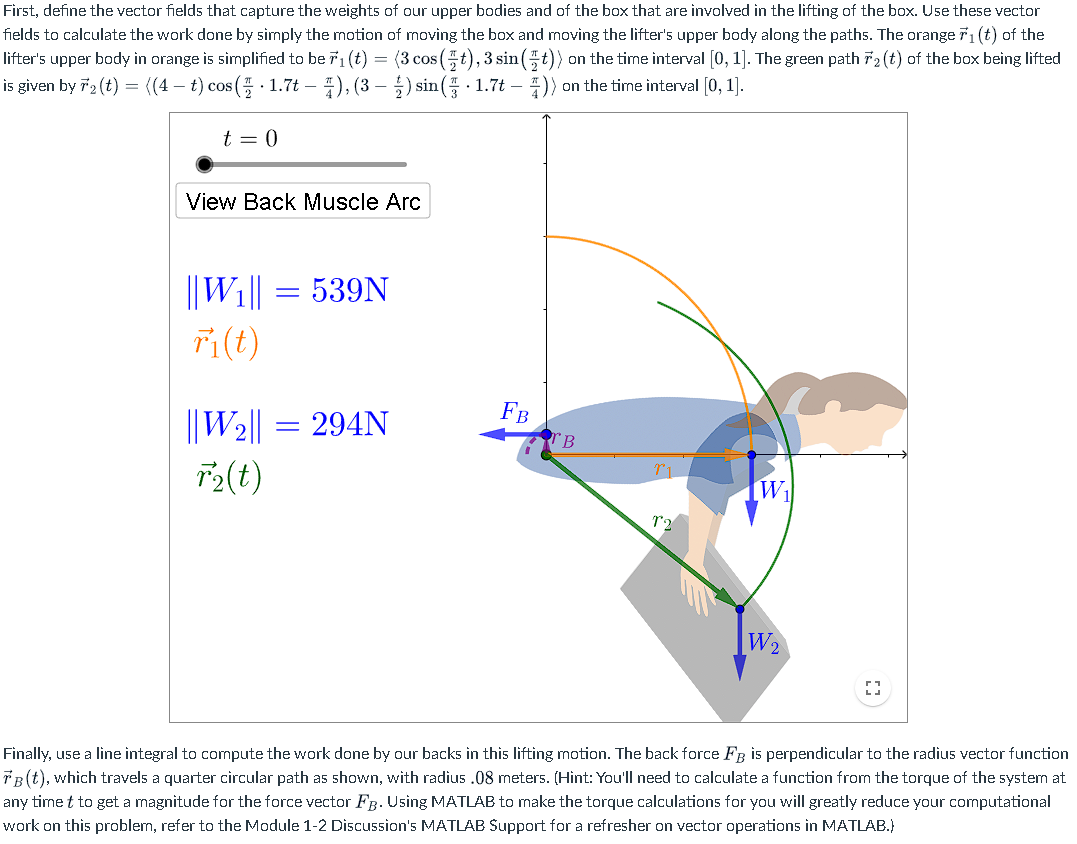
First, define the vector fields that capture the weights of our upper bodies and of the box that are involved in the lifting of the box. Use these vector fields to calculate the work done by simply the motion of moving the box and moving the lifter's upper body along the paths. The orange 71 (t) of the lifter's upper body in orange is simplified to be (t) = (3 cos(t), 3 sin(t)) on the time interval [0, 1]. The green path 72(t) of the box being lifted is given by 72 (t) = ((4 t) cos ( 1.7 - 4), (3 - ) sin ( 1.7- #) > on the time interval [0, 1]. t = 0 View Back Muscle Arc ||W1|| = 539N Fi(t) ||W2|| = 294N FB r B r1 W T2(t) T2 W2 Finally, use a line integral to compute the work done by our backs in this lifting motion. The back force FB is perpendicular to the radius vector function TB (t), which travels a quarter circular path as shown, with radius .08 meters. (Hint: You'll need to calculate a function from the torque of the system at any time t to get a magnitude for the force vector FB. Using MATLAB to make the torque calculations for you will greatly reduce your computational work on this problem, refer to the Module 1-2 Discussion's MATLAB Support for a refresher on vector operations in MATLAB.)