FIX THE ERRORS IN THIS CODE

import numpy as np from scipy.optimize import fsolve from scipy.interpolate import interp2d from typing import Callable class BSMPDESolver: def __init__(self, spot_price, strike_price, maturity, volatility, interest_rate, dividend_yield, payoff_function: Callable): self.S = spot_price self.K = strike_price self.T = maturity self.sigma = volatility self.r = interest_rate self.q = dividend_yield self.payoff_function = payoff_function def solve_pde(self, option_type='European', grid_size=(100, 100)): M, N = grid_size dt = self.T / M dS = (2 * self.S) / N # Initialize grid S_values = np.linspace(0, 2 * self.S, N + 1) t_values = np.linspace(0, self.T, M + 1) grid = np.zeros((M + 1, N + 1)) # Set boundary conditions grid[:, 0] = self.payoff_function(S_values) grid[:, -1] = 0 if option_type == 'European' else self.K - S_values[-1] # Solve the implicit finite difference scheme for i in range(M - 1, 0, -1): A = self._build_coefficient_matrix(grid[i + 1, 1:-1], dS, dt) B = self._build_rhs_vector(grid[i + 1, 1:-1], dS, dt, S_values[1:-1], t_values[i]) grid[i, 1:-1] = fsolve(A, B) return S_values, t_values, grid def _build_coefficient_matrix(self, u_next, dS, dt): sigma2 = self.sigma**2 r = self.r q = self.q alpha = 0.5 * dt * (sigma2 * np.arange(1, len(u_next) + 1)**2 - (r - q) * np.arange(1, len(u_next) + 1)) beta = 1 + dt * (sigma2 * np.arange(1, len(u_next) + 1)**2 + r) gamma = -0.5 * dt * (sigma2 * np.arange(1, len(u_next) + 1)**2 + (r - q) * np.arange(1, len(u_next) + 1)) A = np.diag(alpha, -1) + np.diag(beta) + np.diag(gamma, 1) return A def _build_rhs_vector(self, u_next, dS, dt, S_values, t): sigma2 = self.sigma**2 r = self.r q = self.q b = u_next.copy() b[0] -= 0.5 * dt * (sigma2 * 1**2 - (r - q) * 1) * (self.payoff_function(S_values[0]) - self.payoff_function(S_values[0] - dS)) b[-1] -= 0.5 * dt * (sigma2 * len(u_next)**2 + (r - q) * len(u_next)) * (self.K - S_values[-1]) return b # Example usage: if __name__ == "__main__": def payoff_function(S): return np.maximum(0, S - 100) # Example payoff function (call option) bsm_solver = BSMPDESolver(spot_price=100, strike_price=100, maturity=1, volatility=0.2, interest_rate=0.05, dividend_yield=0.02, payoff_function=payoff_function) S_values, t_values, option_prices = bsm_solver.solve_pde(option_type='European') # Print or visualize the results as needed print(option_prices)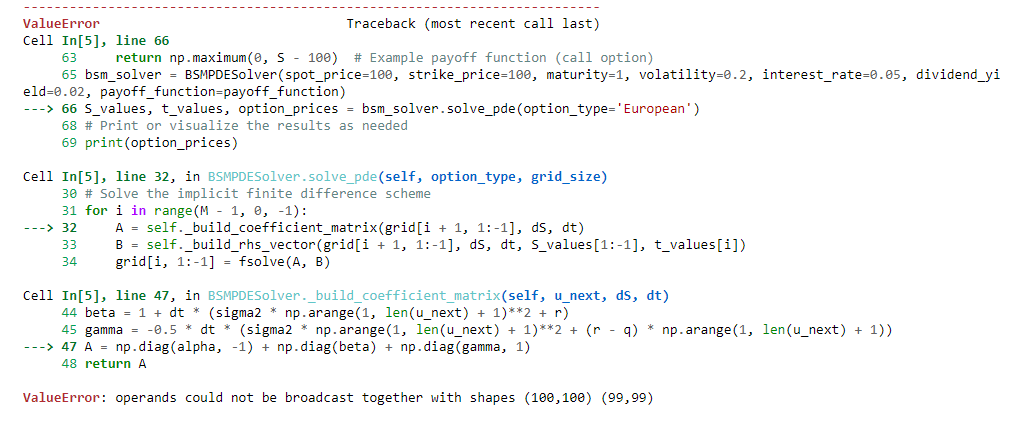

ValueError Traceback (most recent call last) Cell In[5], line 66 63 return np.maximum( , S - 100) \# Example payoff function (call option) 65 bsm_solver = BSMPDESolver(spot_price =100, strike_price =100, maturity=1, volatility=0.2, interest_rate=0.05, dividend_y eld =0.02, payoff_function=payoff_function) ---> 66 S_values, t_values, option_prices = bsm_solver.solve_pde(option_type='European') 68 \# Print or visualize the results as needed 69 print(option_prices) Cell In[5], line 32, in BSMPDESolver.solve_pde(self, option_type, grid_size) 30 \# Solve the implicit finite difference scheme 31 for i in range(M - 1, 0,1) : --> 32 A = self._build_coefficient_matrix(grid[i +1,1:1],dS,dt) 33 B = self._build_rhs_vector(grid[i +1,1:1],dS,dt, S_values[1:-1], t_values[i]) 34grid[i,1:1]=fsolve(A,B) Cell In[5], line 47, in BSMPDESolver._build_coefficient_matrix(self, u_next, dS, dt) 44 beta =1+dt( sigma2 np.arange (1, len (unext )+1)2+r) 45 gamma =0.5dt( sigma 2 np.arange (1, len (unext )+1)2+(rq) np.arange (1, len (u_next)+1)) 48 return A ValueError: operands could not be broadcast together with shapes (100,100)(99,99)