For a protein with two ligand binding sites, the binding polynomial has the general form Q P (1 2k 1 L k 1 k 2 L 2 ) where P is the unbound protein concentration and L is the free ligand concentration The equilibrium constants are defined as k 1 PL P L and k 2 PL 2 PL L a ) Assume k 1 k 2 k 10 and L 0 15 Calculate the fraction of sites bound f B (f B does not equal 0 84) b ) Consider a model where k 1 k and k 2 k If k 10 and L 0 15 calculate the binding fraction 0 1 c ) Assume k 1 k 2 k 10 and L 2 Calculate the fraction of sites bound f B d ) Consider a model where k 1 k and k 2 k If k 10 and L 2 calculate the binding fraction 0 1

The Answer is in the image, click to view ...

Question: For a protein with two ligand binding sites, the binding polynomial has the general form: Q=[P](1+2k 1 [L]+k 1 k 2 [L] 2 ) where

For a protein with two ligand binding sites, the binding polynomial has the general form: Q=[P](1+2k₁[L]+k₁k₂[L]²) where [P] is the unbound protein concentration and [L] is the free ligand concentration. The equilibrium constants are defined as: k₁=[PL]/[P][L] and k₂=[PL₂]/[PL][L] a.) Assume k₁=k₂=k=10 and [L]=0.15. Calculate the fraction of sites bound f_B. (f_B does not equal 0.84).

b.) Consider a model where k₁=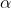 For a protein with two ligand binding sites, the binding polynomial has k and k₂=k . If k = 10 and [L]=0.15 calculate the binding fraction. the general form: Q=[P](1+2k1[L]+k1k2[L]2) where [P] is the unbound protein concentration and =0.1

c.) Assume k₁=k₂=k=10 and [L]=2. Calculate the fraction of sites bound f_B.

d.) Consider a model where k₁= [L] is the free ligand concentration. The equilibrium constants are defined as: k and k₂=k . If k = 10 and [L]=2 calculate the binding fraction. $k1=[PL]/[P][L] and k2=[PL2]/[PL][L] a.) Assume k1=k2=k=10 and [L]=0.15. Calculate the fraction of$ =0.1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Chemistry Questions!

The answer for B is not 0.718 nor 0,2 nor 0.102 nor 0.13 The answer for C is not 0.997 nor 0,2 For a protein with two ligand binding sites the binding polynomial has the general form:...

For a protein with two ligand binding sites the binding polynomial has the general form: Q=[P](1+2k1[L]+k1k2[L]2) where [P] is the unbound protein concentration and [L] is the free ligand...

About measurement of Protein-Ligand binding equilibria by the Ultrafiltration method Question is at last and highlighted, please answer and explain as detail as possible, thanks Introduction...

Use PESTEL ANALYSIS to analyze the 'BEYOND MEAT' case. What is the strategic planning process for BEYOND MEAT? Page 2 - (Whole Foods), Target Corporation, the Kroger 60., Del Taco LLIC (Del Taco),...

You decide to perform ion exchange chromatography next. Howevec, you do not know the isoelectric point (p) of the protein. You decide to perform isoelectric focuting. This is an anaytical technique -...

E-Marketing Plan ( No Plagiarism ) Write an E-marketing Strategic plan for a company or product of your choice. (The company is ICONN Meals and I provided note about them below and also the chapter...

E-Marketing Plan ( No Plagiarism ) Write an E-marketing plan for a company or product of your choice. (The company is ICONN Meals and I provided note about them below and also the chapter notes for...

E-Marketing Plan ( No Plagiarism ) Write an E-marketing plan for a company or product of your choice. (The company is ICONN Meals and I provided notes about them below and also the chapter notes for...

Issue identified in the case. You should consider organizing your report as follows: introduction (Brief summary of the case not more than 150 words) company background (based on data in the case and...

Every year, the students at a school are given a musical aptitude test that rates them from 0 (no musical aptitude) to 5 (high musical aptitude). This year's results were: Aptitude Score 0 1...

Jeff took a couple out to look at the house on the market for 196.7 thousands $. This couple could afford a 10% down payment of the purchase price so they would need to borrow the remaining amount to...

Question 2 4 A perpetual inventory system should be used for overseas inventories only keeps track of the quantity of each item in inventory and where it is located involves counting inventory at...

Write a function void rotate_left(int a[], int size, int n) which will "rotate" array "a", of size "size", n positions to the left. This will rearrange the elements of a by moving them n positions in...

4. Why might one administration interpret and enforce the antitrust laws more strictly than another? How might a change of administrations affect a major monopoly case in progress? LO21.2

LO21.4 Discuss the nature of social regulation, its benefits and costs, and its optimal level.

1. Both antitrust policy and industrial regulation deal with monopoly. What distinguishes the two approaches? How does government decide to use one form of remedy rather than the other? LO21.1, LO21.3