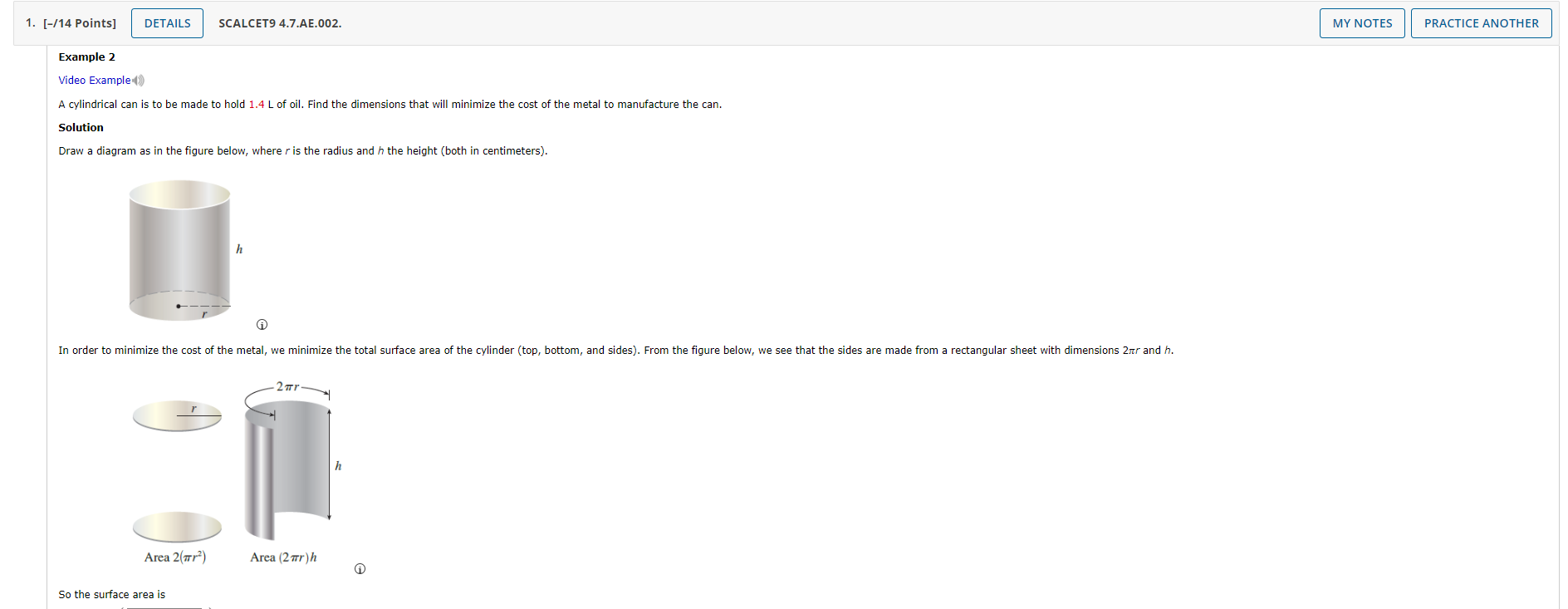
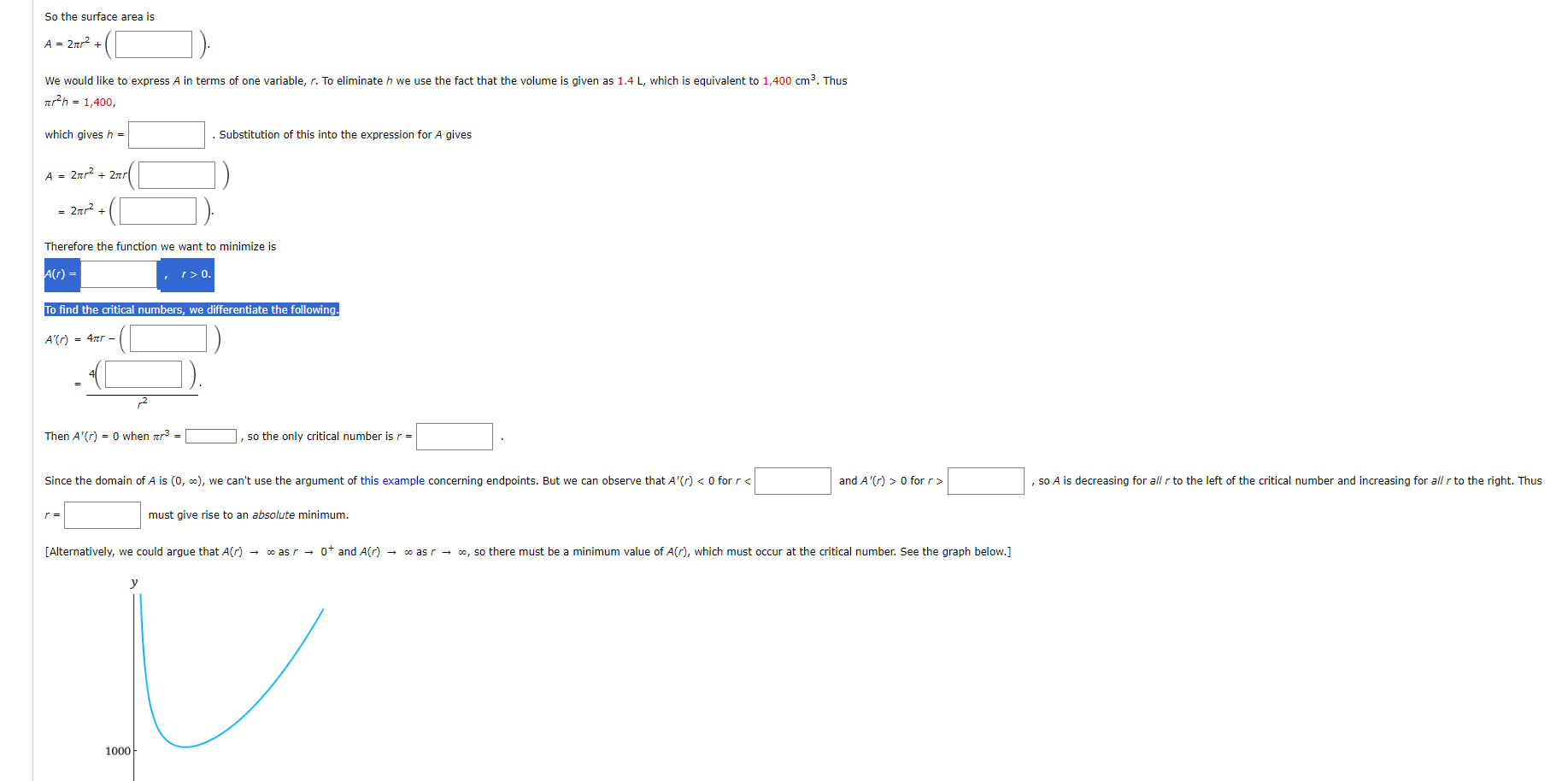
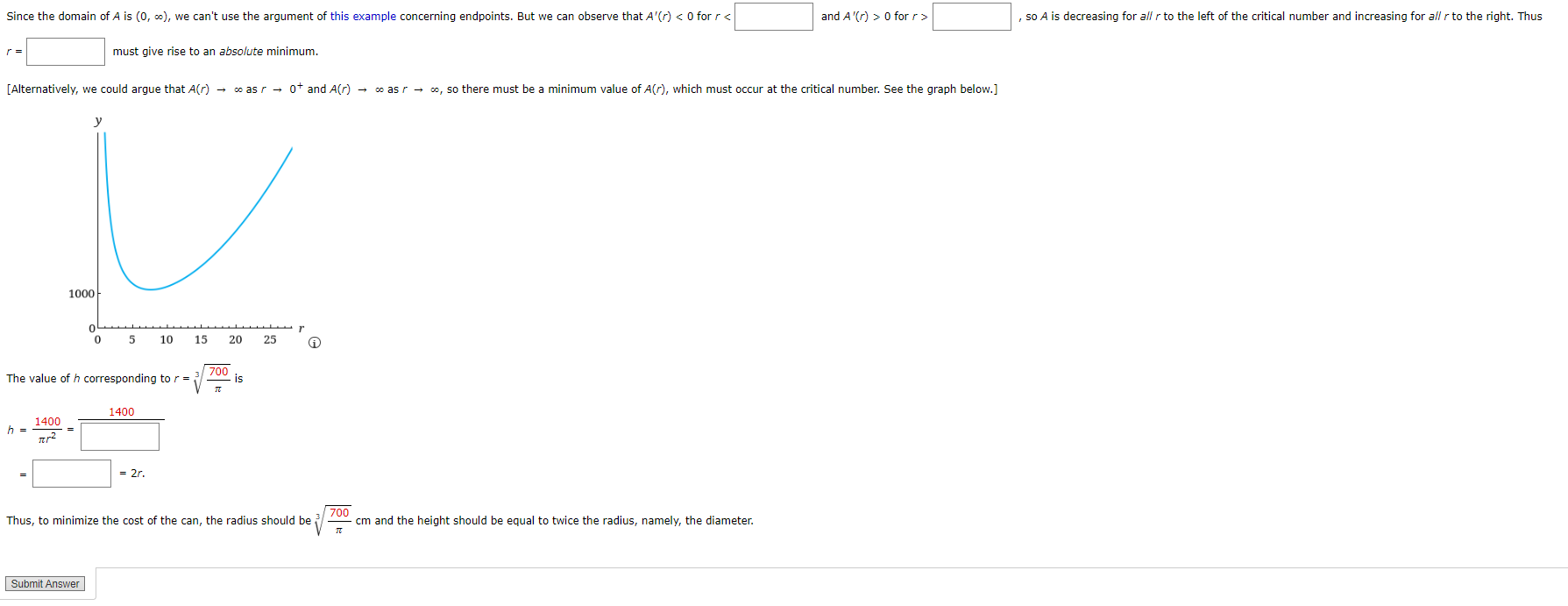
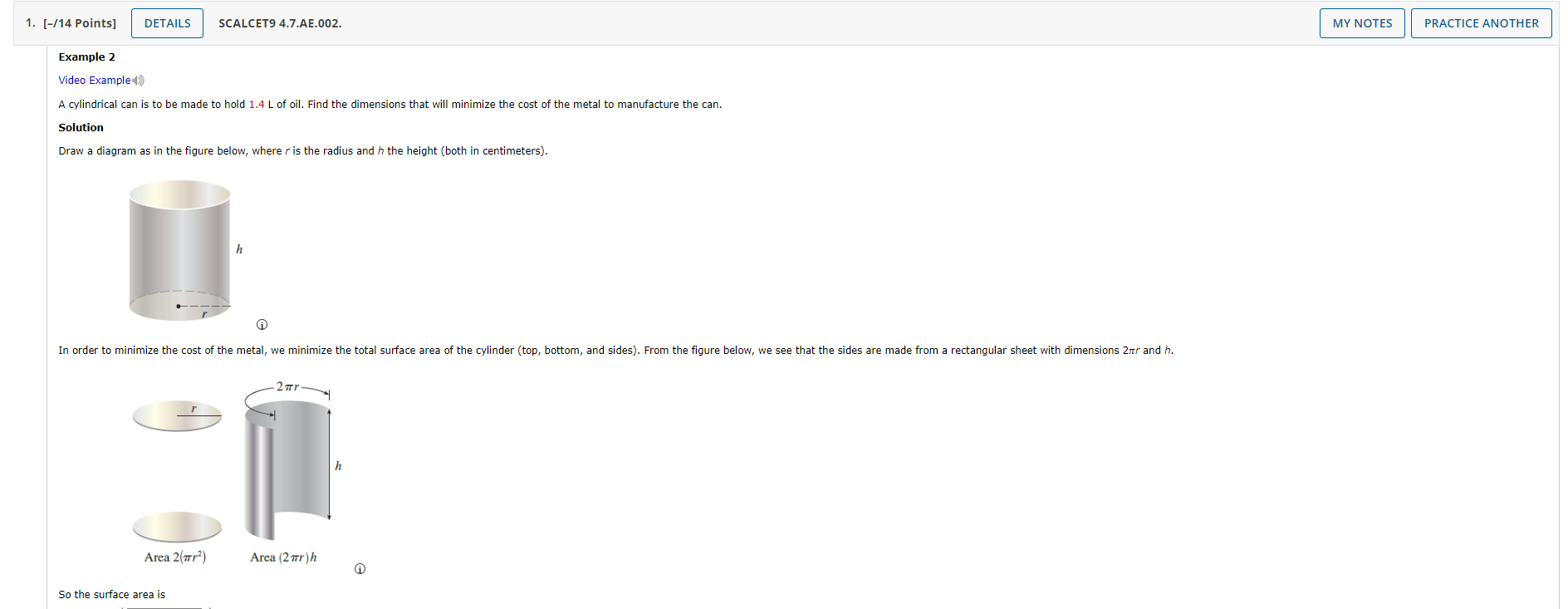
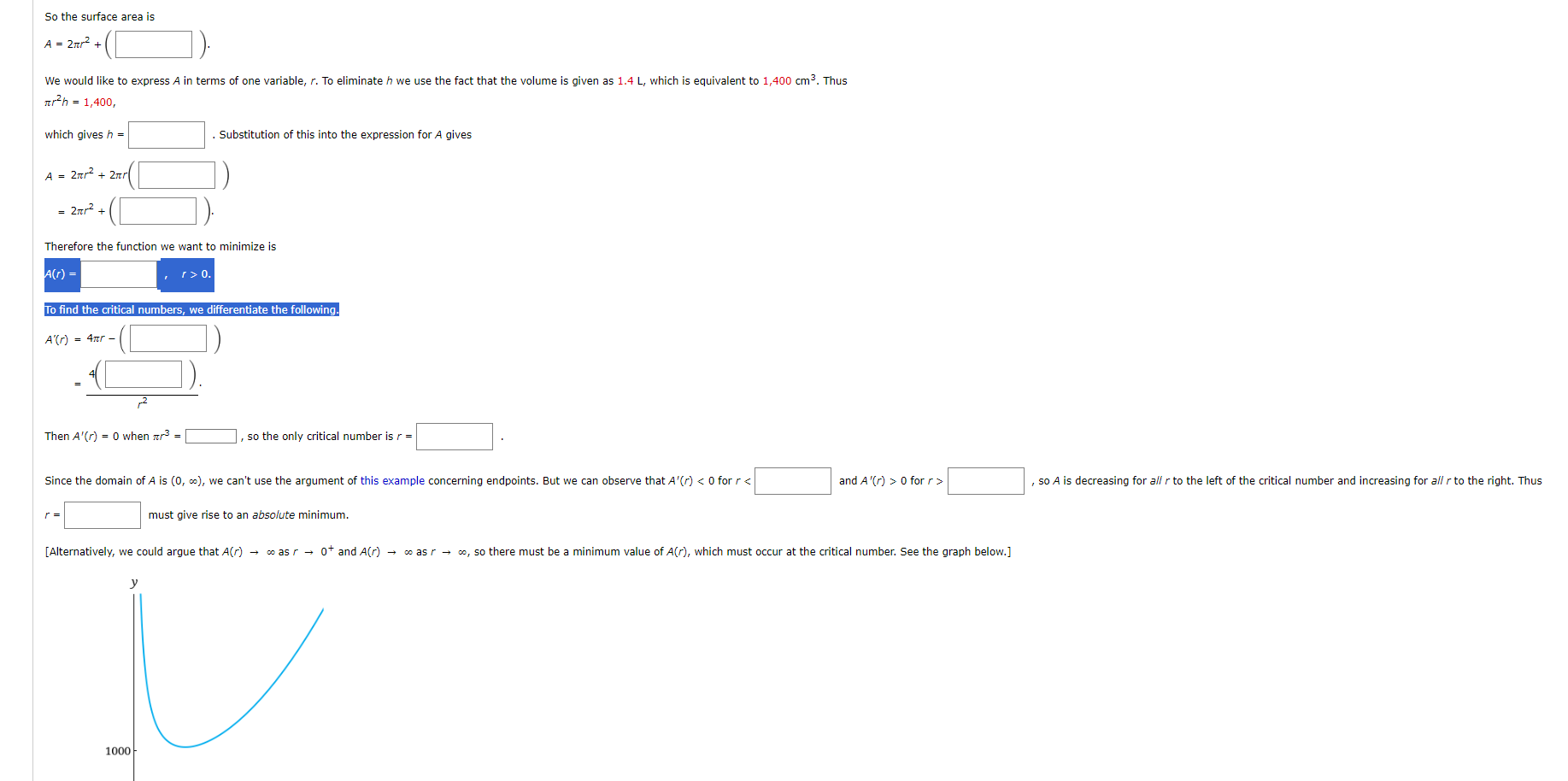
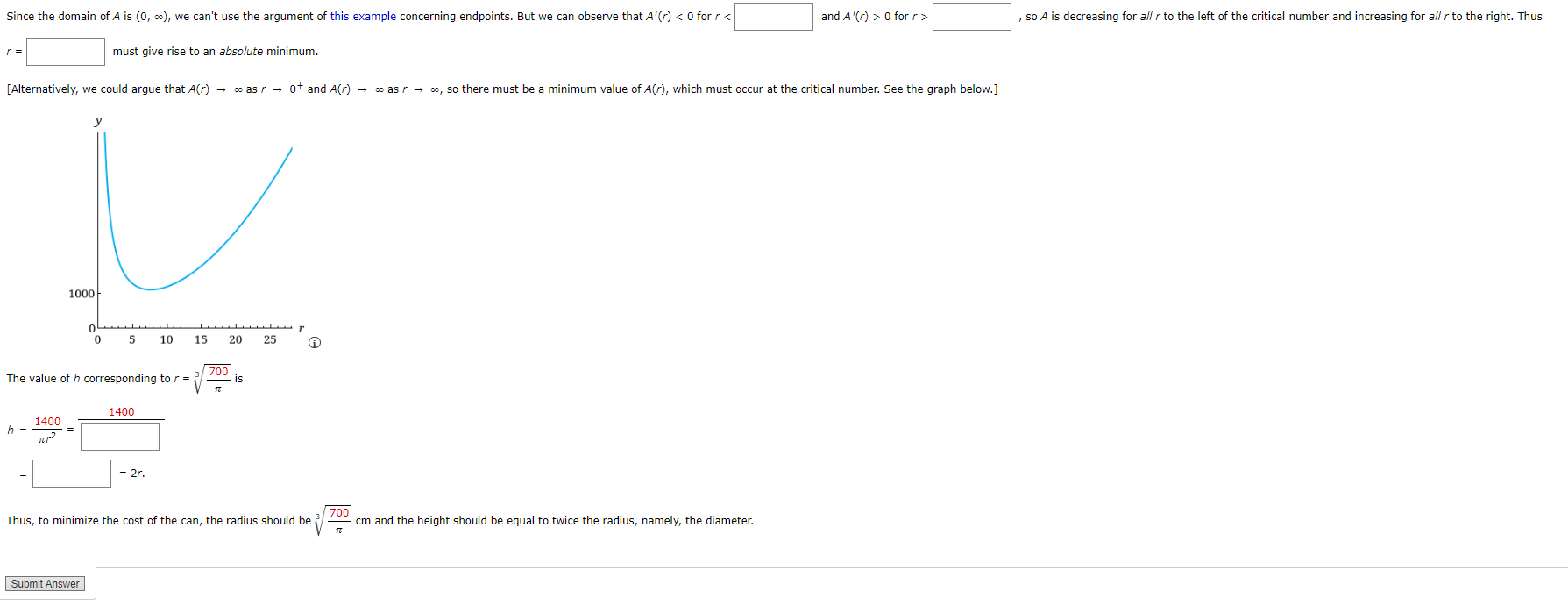
\fSo the surface area is Asst/2% ) We would iike to eXDress A in terms of one valiabie, r. To eiiminate h we use the fact that the Vuiume is given as 1.4 L, which is equivalent to 1,400 Una. Thus flh = 1,400, which gives h = i Substitution of this into the Expression far/4 gives 2s; + 21cr( ) 2s; +( ). ) ii Therefore the function we want to minimize is 3'. 3 n i r'\\ V A V ,2 ThenA'Cr] = u when m3 = , so the only criticai number is r = since the domain of A is (n, so], we can't use the argument at this exampie concerning endpoints. But we can observe that A'(r] o for r > , so A is decreasing For eh r to the left of the critical number and increasing Far 3\" r to the right Thus r = must give rise to an absolute mlhimumi [ulternatively, we could argue that Am A was r e 0+ and/1U) e e as r e as, so there must be a minimum value omcr), which must occur at the cn'ticei number See the graph below] 3' i 1000