Given Information:

Vessel $1$: Unknown flow rate Q$1$ and pressure drop $\backslash$Delta P$=$P$0$P$1$

Vessel $2$: Unknown flow rate Q$2$ and pressure drop $\backslash$Delta P$=$P$1$P$2$

Vessel $3$: Unknown flow rate Q$3$ and pressure drop $\backslash$Delta P$=$P$1$P$3$

P$0=5000$ dyn$/$cm$2$; P$2=$P$3=0$ dyn$/$cm$2$; Vessel $1$: d$1=0\mathrm{.}4$ cm$,$ L$1=10$ cm; Vessel $2$: d$2=0\mathrm{.}28$ cm$,$ L$2=8$ cm; Vessel $3$: d$3=0\mathrm{.}28$ cm$,$ L$3=8$ cm; $\backslash$mu $=1,$

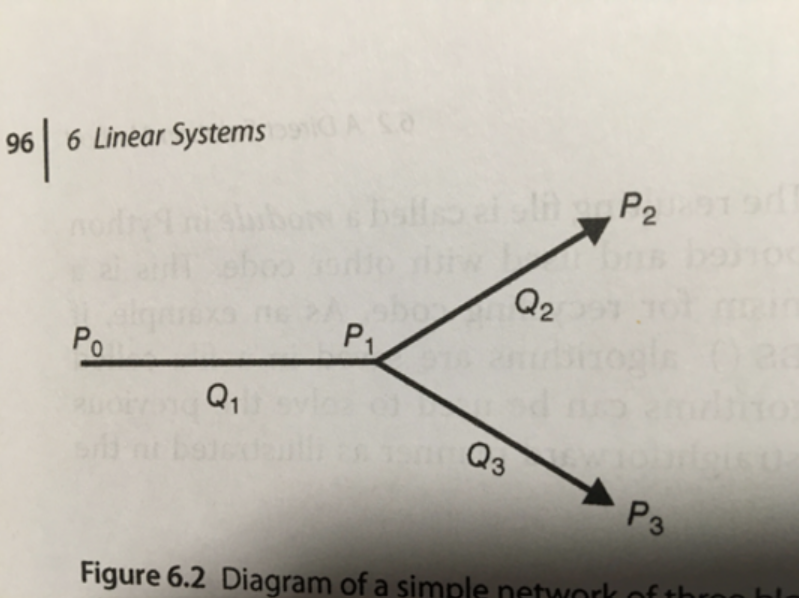
The simplest mathematical model of blood flow assumes that the flow is steady, the vessel walls are rigid, and the blood vessels are straight cylinders. Under these assumptions, the flow inside a vessel can be approximated using the Poiseuille flow solution, which states that the flow rate, $$ Q $,$ through the vessel is proportional to the pressure decrease, $\backslash$Delta P $,$ given by the equation: $\backslash$Delta P $=128.\backslash$mu $.$L$8\backslash$pi d$4$Q $.$ Here, $\backslash$Delta P is the pressure decrease, $\backslash$mu is the viscosity of the blood, L is the length of the vessel, and d is the diameter of the vessel.

Goal: To model flow through three vessels in the below figure.

IN PYTHON CODE:

$1.$ Derive $4$ linear algebraic equations for $4$ unknowns by applying the Poiseuille flow equation and mass balance

$2.$ Write the above Equation in the form of A$.$x $=$ B$,$ where x is a vector of unknown variables. Use Python to write matrix A and vector B

$3.$Determine the element of $3$rd row and $4$th column of the matrix A using Python.