Greedy Algorithm question.

Just not sure on how to start with the algorithm. An explanation about it would be great. A pseudo code would be great too

There is a church whose members attend small group Bible studies every week. One of their goals is for all the church members to get to know each other by having going to a small group with every other member. Also, they want everyone to have a chance to visit everyone elses home. They would like married couples to always go together to the same group.

Your goal is to design and develop a program that will create a list of groups for each week in a way that meets this churchs goals.

Output: The program will produce a list of lists, i.e. a list of groups for each week. Each iteration of your algorithm produces a list of groups for one week in the most evenly distributed way possible. There should be a host for each group, married couples must be together, and everyone (eventually) needs to go to everybody elses home.

Note:

your users should be able to pick the small group size. If the whole community is not an even multiple of the group size, you may assign one more member to as many groups as needed.

Given a list of n people with a size of small groups m, what is minimum number of iterations necessary to accomplish the goal of everybody visiting everybody's house?

What is the time complexity of such algorithm?

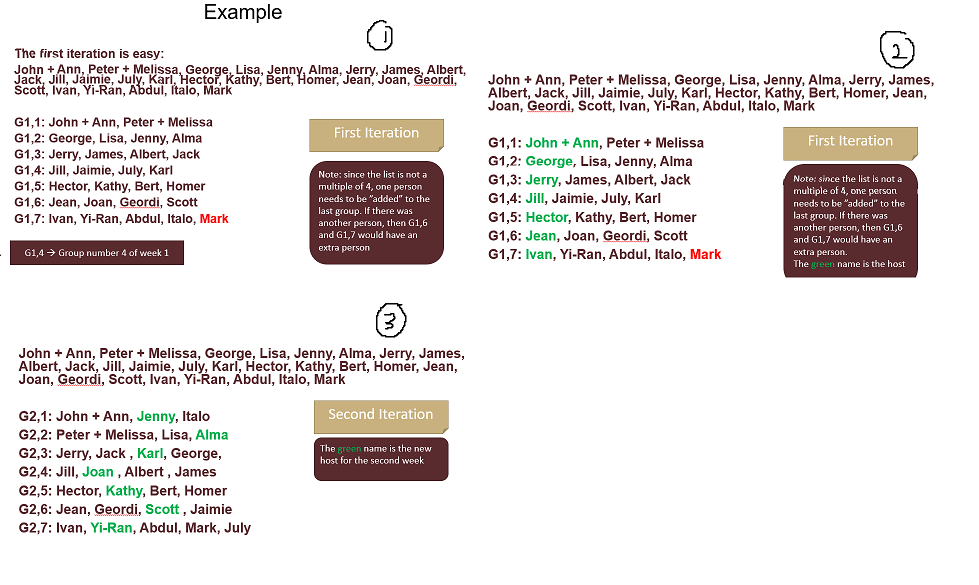
Example 2 The first iteration is easy: John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, ScottIvan, Yi-Ran, Italo, Mark Sache, in vendita de tor Kathy, Bert, Homer, Jean, Joan, Geordi, John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, Jack, Jill, Jaimie, July, Karl, Hector, Kathy, Bert, Homer, Jean, Joan, Geordi, Scott, Ivan, Yi-Ran, Abdul, Italo, Mark First Iteration First Iteration G1,1: John + Ann, Peter + Melissa G1,2: George, Lisa, Jenny, Alma G1,3: Jerry, James, Albert, Jack G1,4: Jill, Jaimie, July, Karl G1,5: Hector, Kathy, Bert, Homer G1,6: Jean, Joan, Geordi, Scott G1,7: Ivan, Yi-Ran, Abdul, Italo, Mark Note: since the list is not a multiple of 4, one person needs to be added to the last group. If there was another person, then G1,6 and G1,7 would have an extra person G1,1: John + Ann, Peter + Melissa G1,2: George, Lisa, Jenny, Alma G1,3: Jerry, James, Albert, Jack G1,4: Jill, Jaimie, July, Karl G1,5: Hector, Kathy, Bert, Homer G1,6: Jean, Joan, Geordi, Scott G1,7: Ivan, Yi-Ran, Abdul, Italo, Mark Note: since the list is not a multiple of 4, one person needs to be added to the last group. If there was another person, then G1,6 and G1,7 would have an extra person The green name is the host 61,4 Group number 4 of week 1 John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, Jack, Jill, Jaimie, July, Karl, Hector, Kathy, Bert, Homer, Jean, Joan, Geordi, Scott, Ivan, Yi-Ran, Abdul, Italo, Mark Second iteration The green name is the new host for the second week G2,1: John + Ann, Jenny, Italo G2,2: Peter + Melissa, Lisa, Alma G2,3: Jerry, Jack, Karl, George, G2,4: Jill, Joan, Albert, James G2,5: Hector, Kathy, Bert, Homer G2,6: Jean, Geordi, Scott, Jaimie G2,7: Ivan, Yi-Ran, Abdul, Mark, July Example 2 The first iteration is easy: John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, ScottIvan, Yi-Ran, Italo, Mark Sache, in vendita de tor Kathy, Bert, Homer, Jean, Joan, Geordi, John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, Jack, Jill, Jaimie, July, Karl, Hector, Kathy, Bert, Homer, Jean, Joan, Geordi, Scott, Ivan, Yi-Ran, Abdul, Italo, Mark First Iteration First Iteration G1,1: John + Ann, Peter + Melissa G1,2: George, Lisa, Jenny, Alma G1,3: Jerry, James, Albert, Jack G1,4: Jill, Jaimie, July, Karl G1,5: Hector, Kathy, Bert, Homer G1,6: Jean, Joan, Geordi, Scott G1,7: Ivan, Yi-Ran, Abdul, Italo, Mark Note: since the list is not a multiple of 4, one person needs to be added to the last group. If there was another person, then G1,6 and G1,7 would have an extra person G1,1: John + Ann, Peter + Melissa G1,2: George, Lisa, Jenny, Alma G1,3: Jerry, James, Albert, Jack G1,4: Jill, Jaimie, July, Karl G1,5: Hector, Kathy, Bert, Homer G1,6: Jean, Joan, Geordi, Scott G1,7: Ivan, Yi-Ran, Abdul, Italo, Mark Note: since the list is not a multiple of 4, one person needs to be added to the last group. If there was another person, then G1,6 and G1,7 would have an extra person The green name is the host 61,4 Group number 4 of week 1 John + Ann, Peter + Melissa, George, Lisa, Jenny, Alma, Jerry, James, Albert, Jack, Jill, Jaimie, July, Karl, Hector, Kathy, Bert, Homer, Jean, Joan, Geordi, Scott, Ivan, Yi-Ran, Abdul, Italo, Mark Second iteration The green name is the new host for the second week G2,1: John + Ann, Jenny, Italo G2,2: Peter + Melissa, Lisa, Alma G2,3: Jerry, Jack, Karl, George, G2,4: Jill, Joan, Albert, James G2,5: Hector, Kathy, Bert, Homer G2,6: Jean, Geordi, Scott, Jaimie G2,7: Ivan, Yi-Ran, Abdul, Mark, July