How do I solve these? Could you also explain how the network

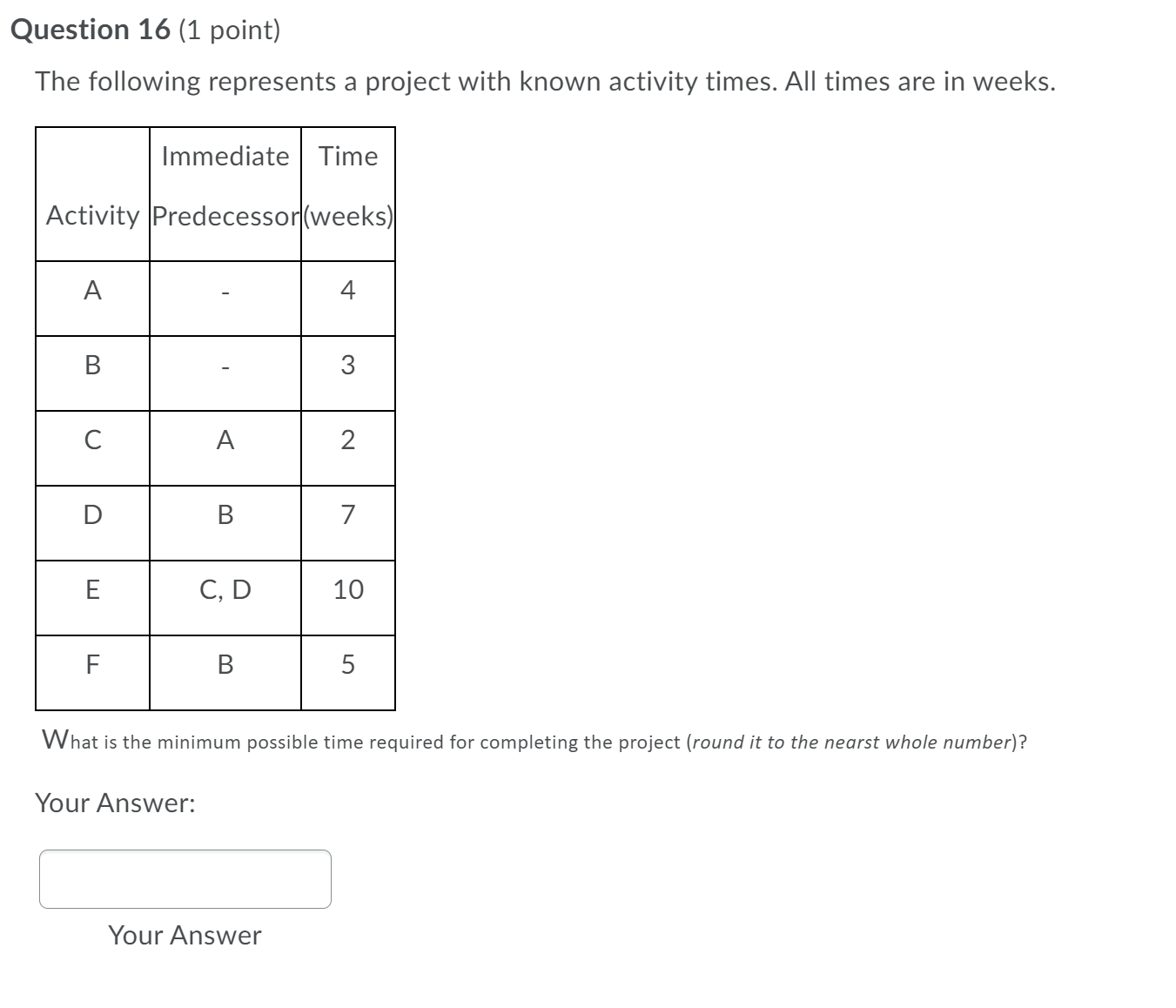
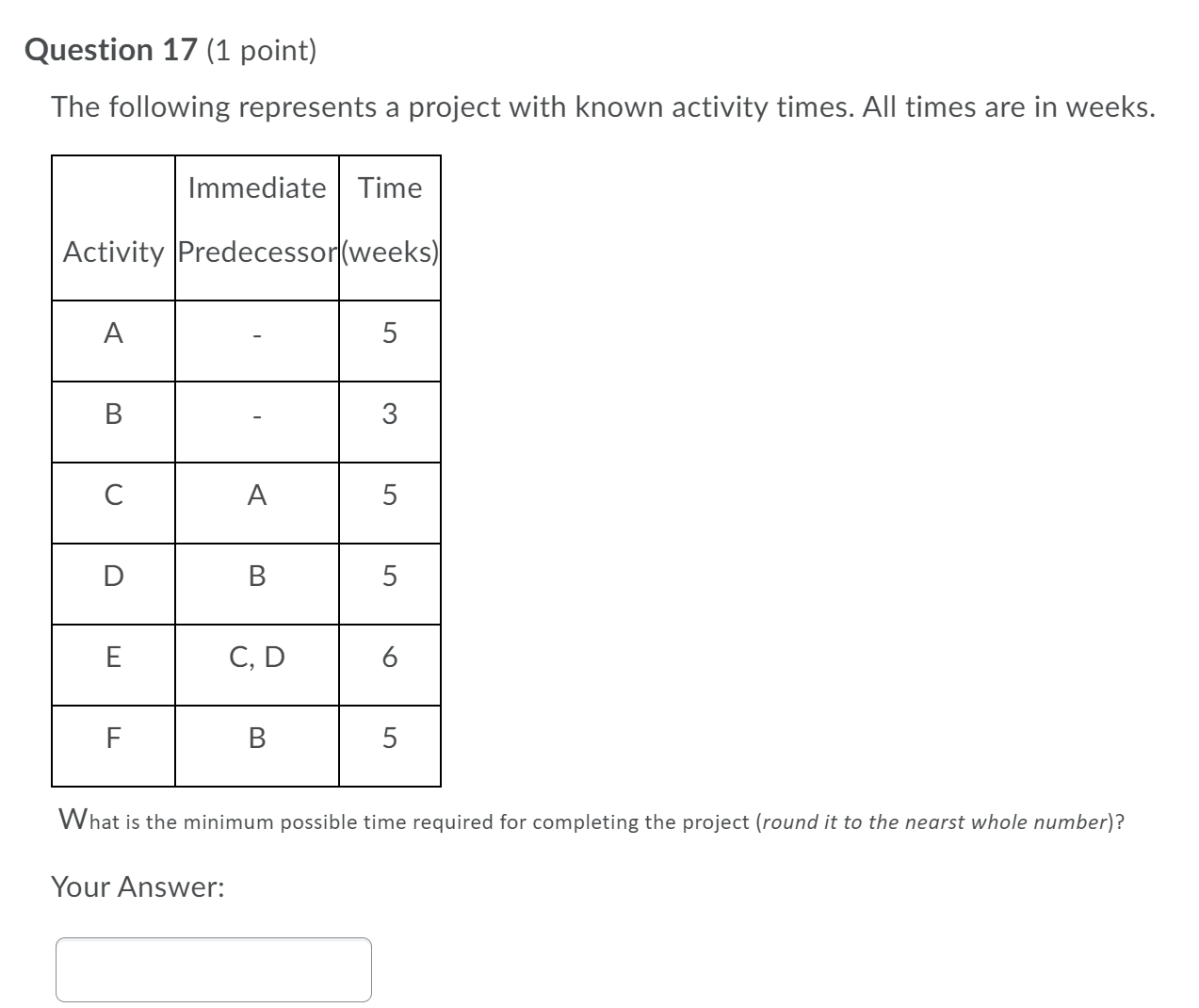
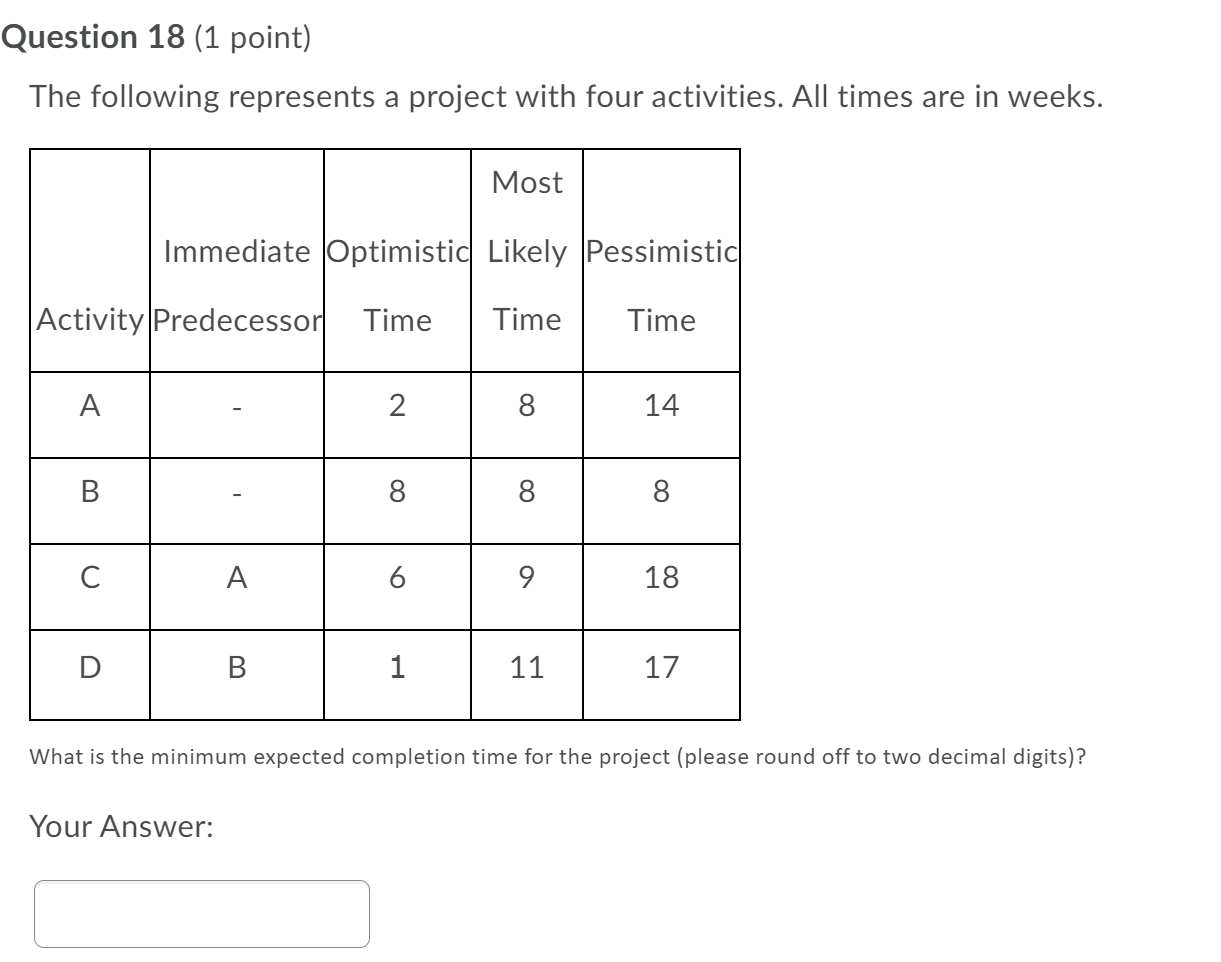
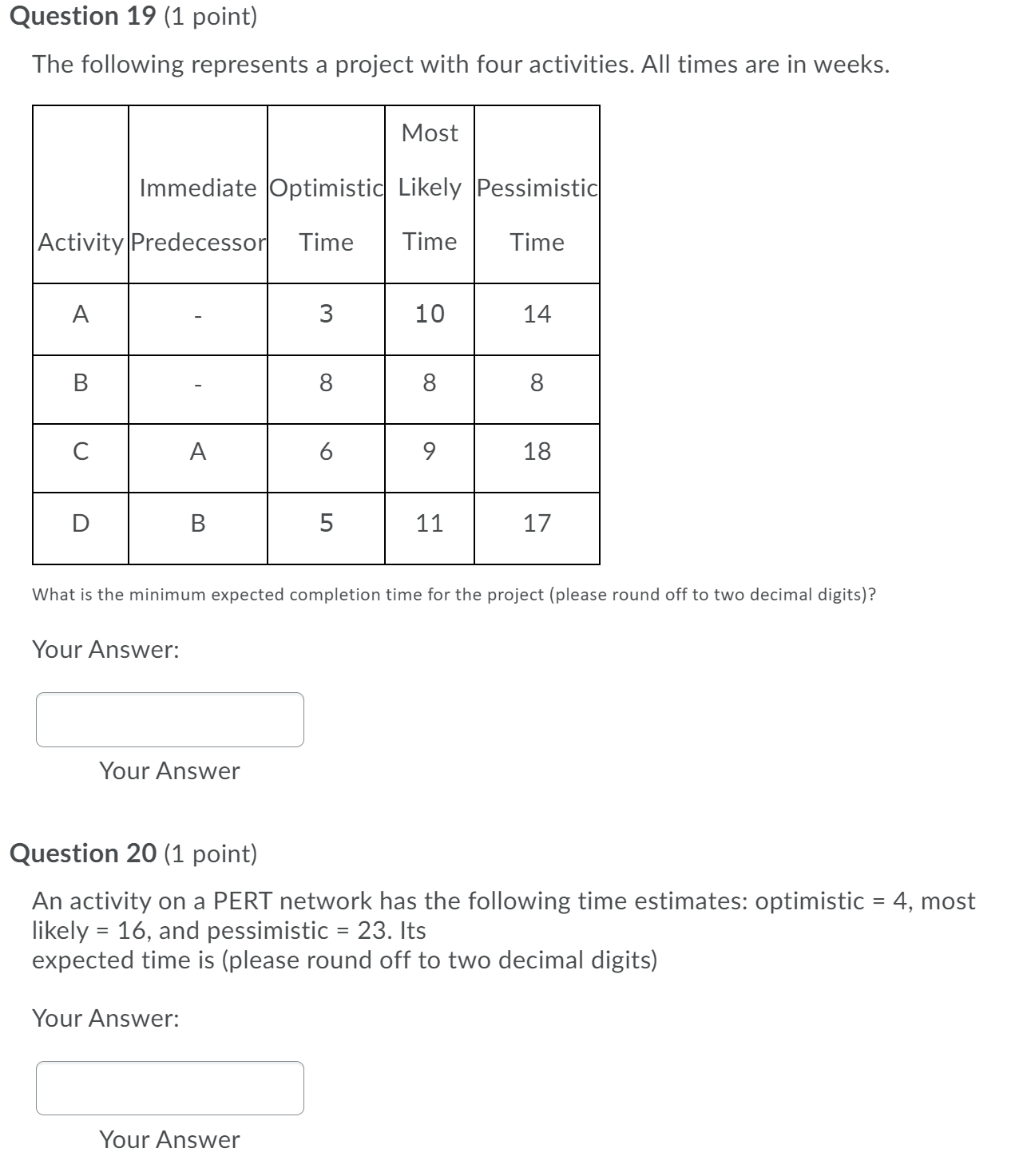
Question 16 (1 point) The following represents a project with known activity times. All times are in weeks. Immediate Time Activity Predecessor(weeks) What is the minimum possible time required for completing the project (round it to the nearst whole number)? Your Answer: Your Answer Question 17 (1 point) The following represents a project with known activity times. All times are in weeks. Immediate Time Activity Predecessor(weeks) What is the minimum possible time required for completing the project (round it to the neorst whole number)? Your Answer: Question 18 (1 point) The following represents a project with four activities. All times are in weeks. What is the minimum expected completion time for the project (please round off to two decimal digits)? Your Answer: Question 19 (1 point) The following represents a project with four activities. All times are in weeks. What is the minimum expected completion time for the project (please round off to two decimal digits)? Your Answer: Your Answer Question 20 (1 point) An activity on a PERT network has the following time estimates: optimistic = 4, most likely = 16, and pessimistic = 23. Its expected time is (please round off to two decimal digits) Your Answer: Your Answer Question 21 (1 point) An activity on a PERT network has the following time estimates: optimistic = 7, most likely = 16, and pessimistic = 23. Its variance is (please round off to two decimal digits) Your Answer: Your Answer Question 22 (1 point) An activity on a PERT network has the following time estimates: optimistic = 3, most likely = 14, and pessimistic = 22. Its standard deviation is (please round off to two decimal digits) Your Answer: Your Answer Question 23 (1 point) A local project being analyzed by PERT has 12 activities, 7 of which are on the critical path. If the estimated time along the critical path is 105 days with a project variance of 25, what is the probability that the project will be completed in 100 days or less? (please answer to four decimal places) Your Answer: Your Answer Question 24 (1 point) A local project being analyzed by PERT has 14 activities, 7 of which are on the critical path. If the estimated time along the critical path is 105 days with a project variance of 25, what is the probability that the project will be completed in 110 days or less? (please answer to four decimal digits) Question 25 (1 point) A project whose critical path has an estimated time of 95 days with a variance of 100 has a 25% chance that the project will be completed before day (please round off to two decimal digits) Your Answer: Your Answer Question 26 (1 point) If an activity whose normal duration is 78 days can be shortened to 34 days for an added cost of $4210, what is the crash cost per period? (please round off to two decimal digits) Your Answer: Your