Question: If we consider two independent Poisson processes with rates 1 and 2 and merge them by recording an arrival whenever an arrival occurs in either

If we consider two independent Poisson processes with rates 1 and 2 and "merge" them by recording an arrival whenever an arrival occurs in either process, then:

The merged process is also Poisson with rate 1 + 2.

Any particular arrival in the merged process has probability 1/(1 + 2) of originating from the first (and 2/(1+2) from the second) process independent of all other arrivals and their origins.

Now consider the following situation: Transmitters A and B independently send messages to a single receiver according to a Poisson process with respective rates A and B. All messages occupy single points in time. The number of words in a message, regardless of the source, is a random variable W independent from everything else:

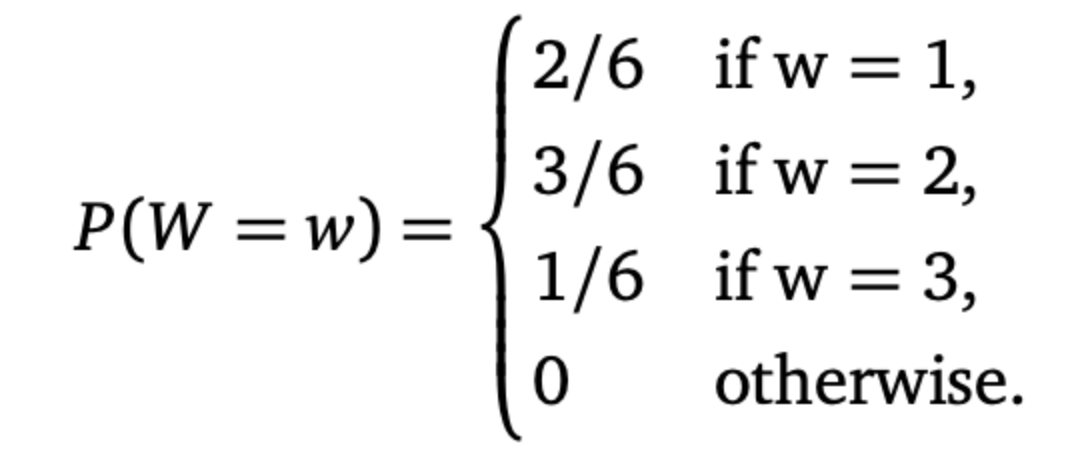
If we consider two independent Poisson processes with rates 1 and 2

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Marla recently inherited $50,000 and is considering two alternatives for investing these funds. Investment A is stock of a C corporation, expected to pay annual dividends of 8 percent. Investment B...

System update. Consider the following queueing system. Customers arrive in pairs according to a Poisson process with rate ? = 1 customer pair/minute. There is one server and room for two customers to...

Consider the following queueing system. Customers arrive in pairs according to a Poisson process with rate ? = 1 customer pair/minute. There is one server and room for two customers to wait in line....

Markov chain distribution. Consider the following queueing system. Customers arrive in pairs according to a Poisson process with rate ? = 1 customer pair/minute. There is one server and room for two...

(a) Prove that for any p = [0, 1] and any integers k and n such that 1 k n, n -p)--(-)- (-1)p(1 - p). n (m) p (1 - p)" m=k = m=k For this you may consider a binomial process with parameter p and its...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Describe the differences in the results between the groups in the study and support your description with examples from the study. Abstract Background:Nurses who work the night shift often experience...

Identify the potential weaknesses of the data analysis methods used. Support your discussion with examples from the study. Background:Nurses who work the night shift often experience high levels of...

Explanatory Variable(s) What is/are the explanatory variable(s)? and Response Variable(s) What is/are the response variable(s)? ABSTRACT Background: Nurses who work the night shift often experience...

Identify the limitations of the study design used and explain why those limitations exist. BACKGROUND Researchers began studying night-shift sleepiness in the 1950s; and physiologic evidence of...

In the spreadsheet, the prompts for entering data are in column A. The user enters the data in column B. a. Write the spreadsheet formula that will calculate the radius in cell B4. b. Write the...

Elsher Implements Company had sales revenue of $785,000 in 20x2. Pertinent data for its only product in 20Xx2 included the following: Click the icon to view the data). Requirements 1. Prepare a...

( 5 points ) Find the derivatives of the following functions. ( a ) g ( x ) = e 2 x 2 x

The condensed income statement for the International Division of King Industries Inc. is as follows (assuming no service department charges): Sales .............. $1,200,000 Cost of goods sold...

A round solid cylinder made of a plastic material ( a = 6 x 10 -7 m 2 /s) is initially at a uniform temperature of 20 o C and is well insulated along its lateral surface and at one end. At time t =...

A long pyroceram rod of diameter 20 mm is clad with a very thin metallic tube for mechanical protection. The bonding between the rod and the tube has a thermal contact resistance of R t.c = 0.12 m ...

Variable costing and absorption costing, the All-Fixed Company (R. Marple, adapted) It is the end of 2011. The All-Fixed Company began operations in January 2010. The company is so named because it...

Circuit boards are mounted to interior vertical surfaces of a rectangular duct of height H = 400 mm and length L = 800 mm. Although the boards are cooled by forced convection heat transfer to air...

Honest Al's Used Cars wants to predict how many cars are sold each month. He has collected data for 12 months. He needs your help in analyzing the data uring moving averages B 1 2 Time Period Number...

=+would you use if a major client wanted you to demonstrate your CSR commitment?

=+5. Have a look at this article by Timothy Ogden (http://www.millermccune.com/business_economics/ computer-error-1390).317 What are some of the criticisms of OLPC?

=+Do you think it is an effective way of improving the education of children in developing countries?