Question: if you could answer this! its the same questions just different numbers. ignore the things filled in already. thank you so much The Hills County,
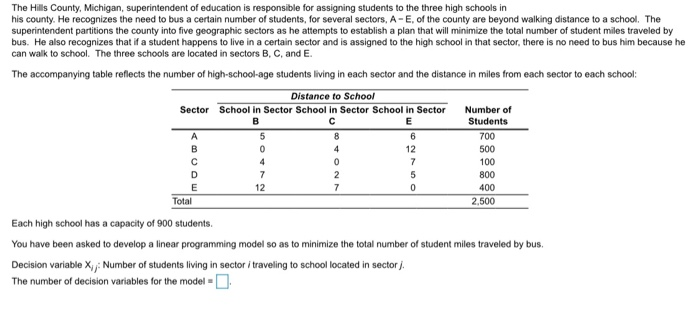
 if you could answer this! its the same questions just different numbers. ignore the things filled in already. thank you so much
if you could answer this! its the same questions just different numbers. ignore the things filled in already. thank you so much Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


