I'm having some problems with this question:

Directed graph G is represented by the adjacency matrix below. Draw the directed graph G and run the strongly connected components algorithm on it (use the algorithm from p.94 of the textbook). When doing DFS on G R : whenever there is a choice of vertices to explore, always pick the one that is alphabetically first. Answer the following questions. (Recall that 1 in row i and column j means that there is an edge from vertex i to vertex j. For instance, there is an edge from A to C.)

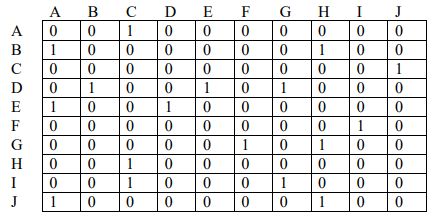
I got the following graph is this correct?

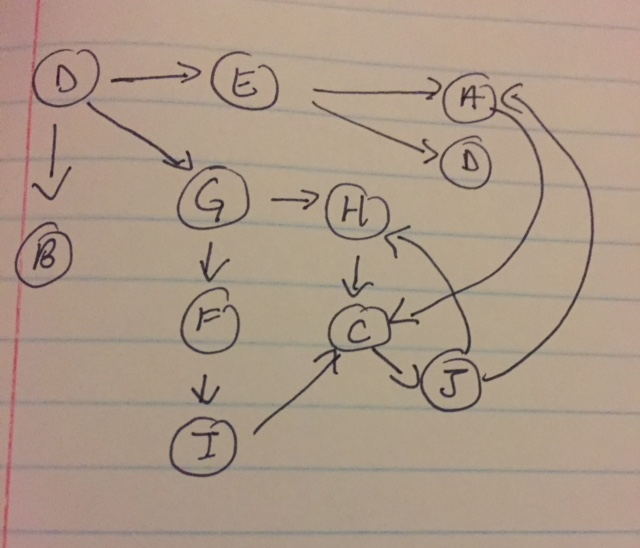
After I do that I'm supposed to do the following:

(a) In what order are the strongly connected components (SCCs) found? (Not sure what they mean by this)

(b) Which are source SCCs and which are sink SCCs? (It's a sink if it doesn't have any edges leaving from a node and it's a source if it doesn't have any other nodes pointing at it. Is this the right definition? If so should I look for these on the graph or on the reverse graph (GR)?

(c) Draw the metagraph (each meta-node is an SCC of G). (How can I tell when something is a strongly connected component?)

(d) What is the minimum number of edges you must add to this graph to make it strongly connected?

J 0 0 0 0 0 0 0 0 0 10000010000 H0-0000-100-1 G000-00-0010 F0000001000 E0001000000 D0000-00000 CI-000000-10 B000-000000 A01-00-000 01 ABCDEFGHIJ