import numpy as np import matplotlib.pyplot as plt

def mysin(x, tol=1e-8): """ compute sin(x) by summing taylor expansion at 0,

sin(x) = x - x^3/3! + x^5/5! +.... + (-1)^k*x^(2k+1)/(2k+1)! + ...

up to accuracy of tol, i.e. break out of loop when the |new term to be added|

def mycos(x, tol=1e-8): """ compute cos(x) by summing taylor expansion at 0,

cos(x) = 1 - x^2/2! + x^4/4! +.... + (-1)^k*x^(2k)/(2k)! + ...

up to accuracy of tol, i.e. break out of loop when the |new term to be added|

def mysin_mod(x, tol=1e-8): """ compute sin(x) by summing taylor expansion at x0=j*pi, (for some integer j such that j*pi is closest to x), if j is even, then sin(x) = (x-x0) - (x-x0)^3/3! + (x-x0)^5/5! +.... + (-1)^k*(x-x0)^(2k+1)/(2k+1)! + ... if n is odd, multiply the above by -1. """ #if you can, apply the more efficient 'updating' method instead of direct sum term-by-term

def mycos_mod(x, tol=1e-8): """ compute cos(x) by summing taylor expansion at x0=j*pi, (for some integer j such that j*pi is closest to x), if j is even, then cos(x) = 1 + (x-x0)^4/4! + (x-x0)^8/8! + (x-x0)^12/12! + (x-x0)^16/16! + ... - (x-x0)^2/2! + (x-x0)^6/6! + (x-x0)^10/10! + ... ) if j is odd, multiply the above by -1. """ #if you can, apply the more efficient 'updating' method instead of direct sum term-by-term

def plot_sincos(xarr = np.linspace(-3*np.pi, 3*np.pi, 600)): """ the input xarr is the array that contains all the x values for the plot of funtions """ #add code below to plot the functions mysin() and mycos() #using the format/style specified in the project PDF

#save the plot to a file for submission plt.savefig('sincos_'+str(len(xarr))+'_'+str(int(max(xarr)))+'.png') plt.show()

def plot_sincos_mod(xarr = np.linspace(-3*np.pi, 3*np.pi, 600)): """ the input xarr is the array that contains all the x values for the plot of funtions """ #add code below to plot the functions mysin_mod() and mycos_mod() #using the format/style specified in the project PDF

#save the plot to a file for submission plt.savefig('sincos_'+str(len(xarr))+'_'+str(int(max(xarr)))+'_mod.png') plt.show()

Will thumbs up if anyone can help me with this problem!

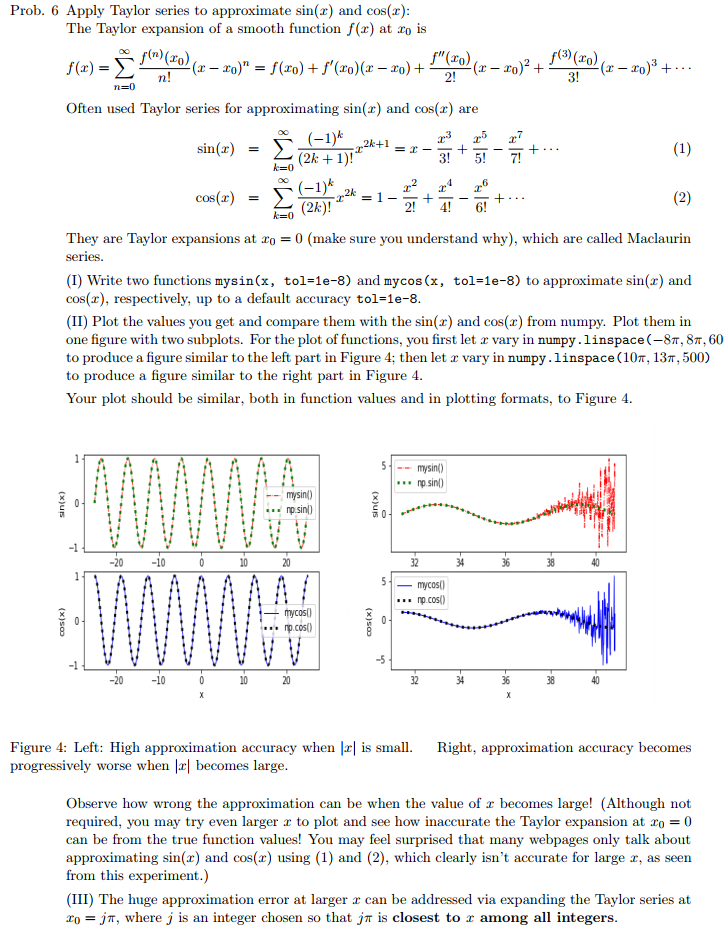
Prob. 6 Apply Taylor series to approximate sin(z) and cos(r) The Taylor expansion of a smooth function f(z) at zo is ofm(o) f"(xo) 2! Often used Taylor series for approximating sin() and cos(z) are sin( - (-1)* 2k cos( - They are Taylor expansions at ro-0 (make sure you understand why), which are called Maclaurin series (I) Write two functions mysin(x, tol-1e-8) and mycos(x, tol-1e-8) to approximate sin( and cos(x), respectively, up to a default accuracy tol-1e-8 (II) Plot the values you get and compare them with the sin(z) and cos() from numpy. Plot them in one figure with two subplots. For the plot of functions, you first let x vary in numpy . linspace ( 8.8T. 60 to produce a figure similar to the left part in Figure 4: then let x vary in numpy . linspace (10T, 13T, 500) to produce a figure similar to the right part in Figure 4 Your plot should be similar, both in function values and in plotting formats, to Figure 4. mysin() np.sin mysin) np sin -10 20 34 mycos .np.cos) mycos0 mp.cos 20 32 34 38 Figure 4: Left: High approximation accuracy when lr is small. Right, approximation accuracy becomes progressively worse when r becomes large Observe how wrong the approximation can be when the value of r becomes large! (Although not required, you may try even larger r to plot and see how inaccurate the Taylor expansion at ro0 can be from the true function values! You may feel surprised that many webpages only talk about approximating sin(x) and cos(r) using (1) and (2), which clearly isn't accurate for large r, as seen m this experiment.) (III) The huge approximation error at larger x can be addressed via expanding the Taylor series at ojT, where j is an integer chosen so that jm is closest to r among all integers