LetA=101321101 I) Find the eigenvalues of A. Then determine the canonical forms of Jordan

Possible of A (at permutation of the blocks ready).

Ii) Find the canonical form of Jordan J of A. Give an invertible S matrix such

That S¹AS = J and explicitly calculate its inverse S¹.

Iii) Calculate e^tJ, t R.

Note: Reference MAT3341 1: Algebra linear applied

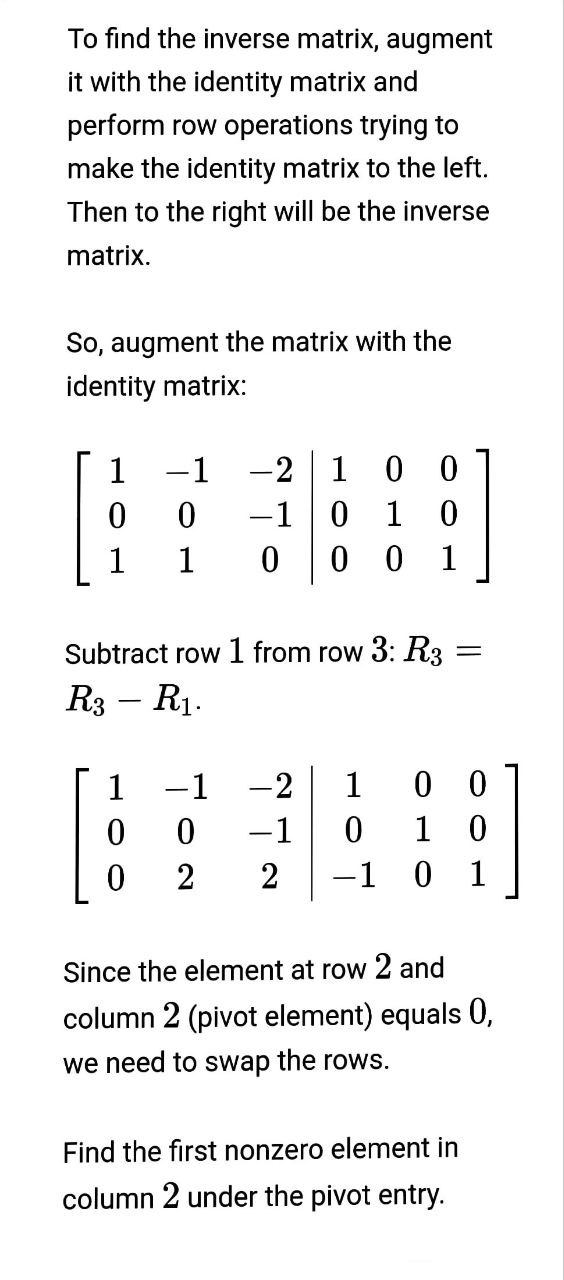
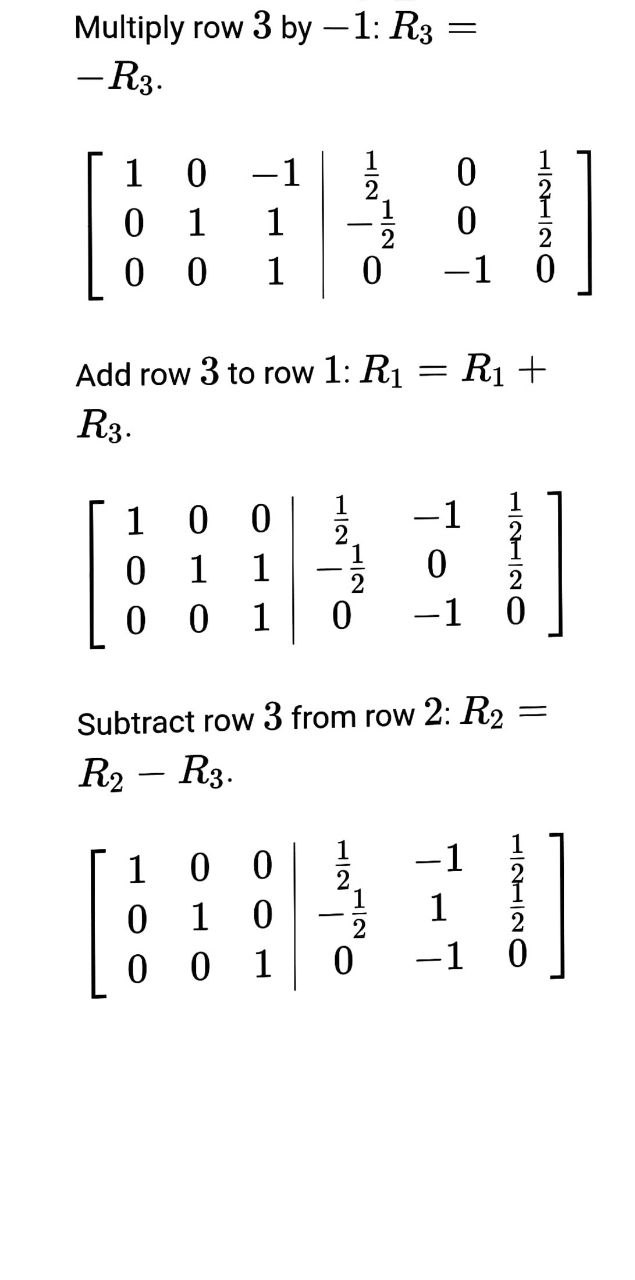
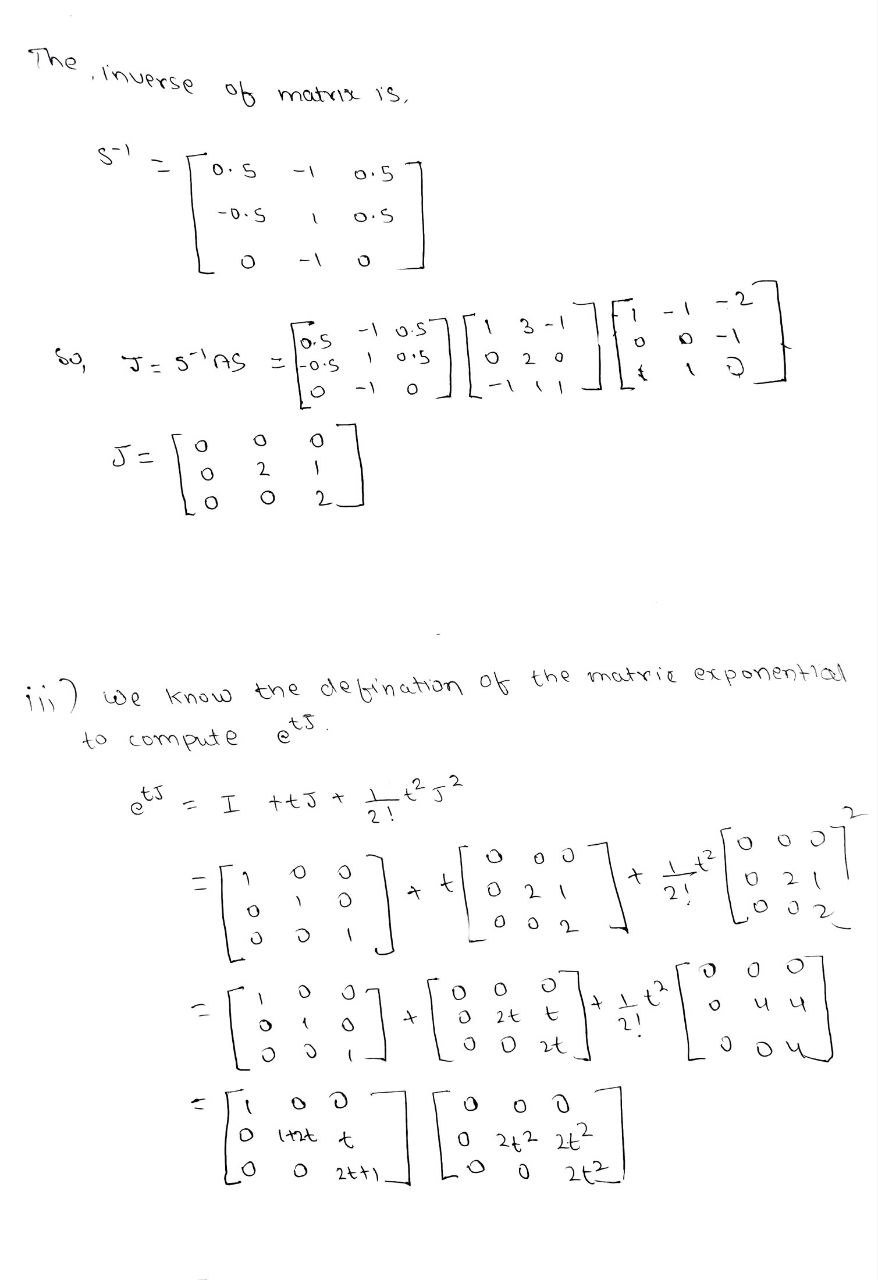
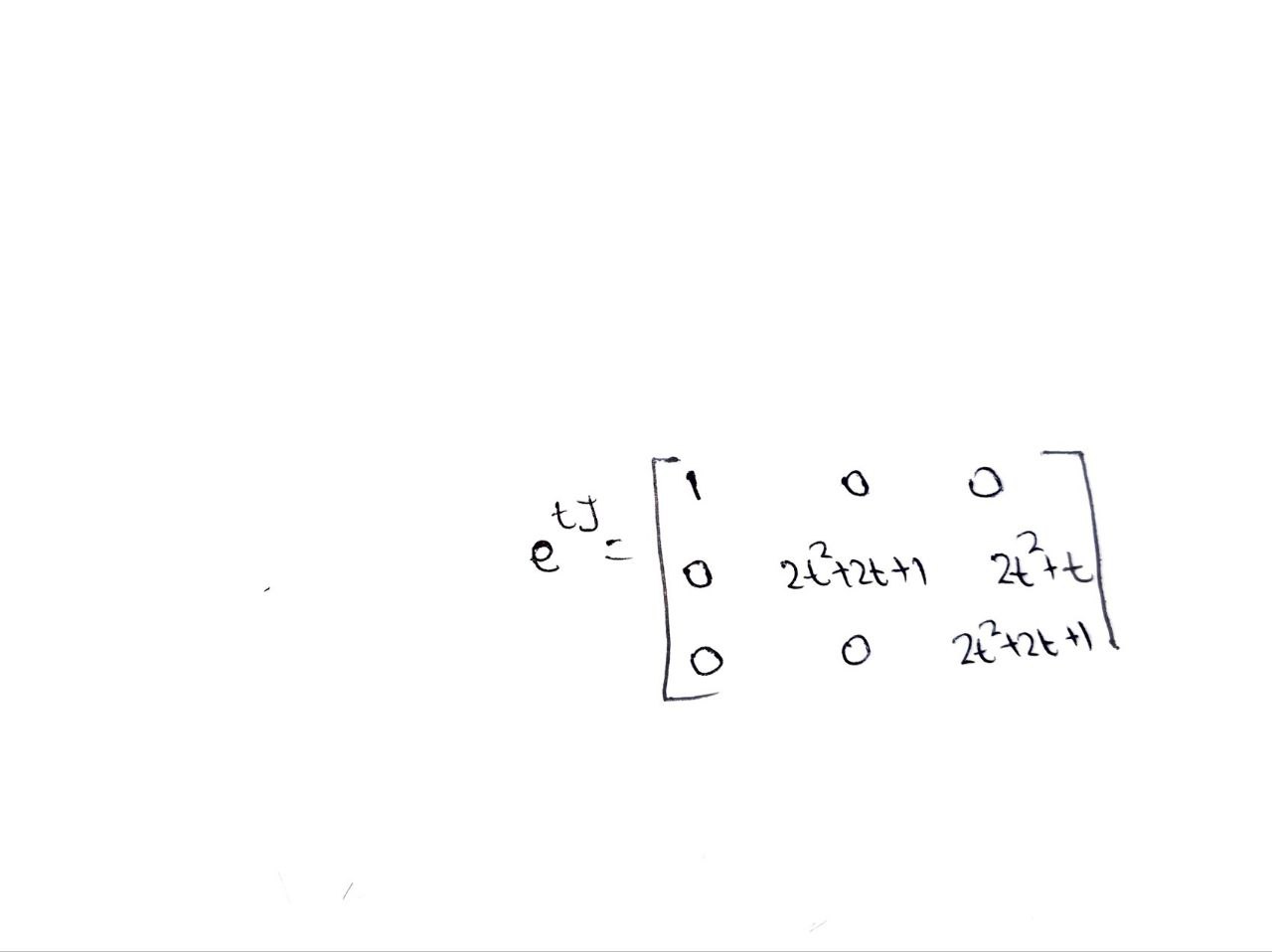
we have , U, O Now we have to find the generalised eigenvector for this matrix . The generalised eigenvector is O So , required matrixe S = O OTo find the inverse matrix, augment it with the identity matrix and perform row operations trying to make the identity matrix to the left. Then to the right will be the inverse matrix. So, augment the matrix with the identity matrix: 1 -1 =21 0 O 0 0 -1/0 1 0 1 1 01]0 01 Subtract row 1 from row 3: R3 = R3 R;. 1 1 =2 1 @ @ O 0 -1]0 1 O 0 2 2 | -1 0 1 Since the element at row 2 and column 2 (pivot element) equals 0, we need to swap the rows. Find the first nonzero element in column 2 under the pivot entry. The first nonzero element is at row Swap the rows 2 and 3: O -1 -2 1 0 2 2 -1 0 OO O -1 0 10 Divide row 2 by 2: R2 = R2 2 -2 1 O 1 ONH O 0 HO 0 -1 0 Add row 2 to row 1: R1 = R1 + R2. 1 0 -1 2 01 1 ONIHOP HOO 0 O -1\fThe inverse of matrix is, 0 . 5 0 .5 - D . S O .5 O - 1 O 60, J = S" AS O. - 1 1 - 2 - O 'S 0 O O O O J = O ONO in ) we know the defination of the matric exponential to compute ots. t = I ttJ+ - + 2 - 2 21 O O 0 OO O O 2 21 O 2 0 2 O O O O O O O 2t t O u 4 O 2t O Itht t 0 2+2 262 0 2t+1 O 0 2+2\f