MATLAB code assignment

Image Enhancement Using Intensity Transformations

The focus of this project is to experiment with intensity transformations to enhance an image. Download phoenix lander.tif and enhance it using 1. The log transformation of Note 3, page 8:

g = c log(1 + f )

2. A power-law transformation of the form shown in Note 3, page 10.

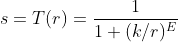
Hint: you might want to use the function: g = stretchTransform(f,varargin)

In (1) the only free parameter is c, but in (2) there are two parameters, k and E for which values have to be selected. As in most enhancement tasks, experimentation is a must. The objective of this project is to obtain the best visual enhancement possible with the methods in (1) and (2). Once (according to your judgment) you have the best visual result for each transformation, explain the reasons for the major differences between them.

As a minimum, your report should include For problem (1): 1. problem description, your name, date 2. the original image, 3. the enhanced image, 4. What is your pick for the parameter c? 5. all codes you applied

For problem (2): 1. problem description, your name, date 2. the original image, 3. the enhanced image, 4. What is your pick for the two parameters, k and E? 5. all codes you applied

I would be happy if you add some explnations for each step.

Thank you in advance.

- Tools for dynamic range compression - Logarithmic transformation: g=clog(1+double(f)) Example: - Fourier spectrum has values in the range [0,106]. - If displayed on a monitor, values would be scaled linearly to 8 bits. High values would dominate the display, so visual details would be lost. - Apply log transformation, the dynamic range is [0,14] : loge(106)=6ln(10)=13.8 - Bring values back to [0,255] range: g=im2uint8(mat2gray(g)) 3: Contrast-Stretching Transformations s=T(r)=1+(k/r)E1 - g=1./(1+(k./( double(f) +eps)).E) - Stretch levels is k - E controls the slope of the function T - Expand narrow range of input intensity k into a wide range of light levels See how varargin is used in the function g= stretchTransform(f, varargin) for computing g=1./(1+(k./f).E), then test the following codes: - f=im2 double(imread('bonescan.tif')); - k=mean2(f) - E=0.9 - figure; imshow(f); figure; imshow(g); - r=0:1/255:1; - T=1./(1+k./r).E - figure; plot(T) Now you try: g=stretchTransform(f);figure;imshow(g)