MATLAB HOMEWORK__SHOW CODE

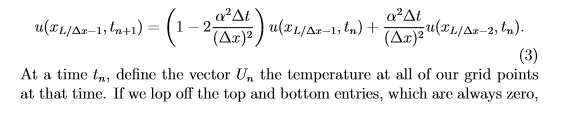
Problem 1: The Heat Equation We spent two weeks studying ordinary differential equations. We will now numerically solve a partial differential equation: the heat equation. Consider a metal rod of length L. The temperature of the rod at a point x (where x is between 0 and L) is given by u(x, t). That is, the temperature changes both along the rod, and with time! A physical model for how the temperature of the rod changes with time is the partial differential equation (L ol where is a constant related to the heat conductance of the bar, and is simply a way of saying "the first derivative of u with respect to time." In order to characterize the behavior, we need both boundary conditions and an initial condition For this problem, we assume the ends of the rod are held at a constant zero temperature. Mathematically, this translates to u(0, t)-0 for all time and u(L,t) 0 for all time. Think of it as if the ends of the rod are sitting in ice baths that are kept at a constant temperature, due to the constantly melting ice Finally, we need to have an initial condition. That is, we need to know what the temperature of the rod is everywhere along it at the starting time! Obviously, the ends are at zero, as they always are, but the initial tempera- ture of the interior points must be provided as an initial function of x (x) Thus, u(z,0) = (z) for all z. Putting all of this together gives us the full problem statement of the heat equation Problem 1: The Heat Equation We spent two weeks studying ordinary differential equations. We will now numerically solve a partial differential equation: the heat equation. Consider a metal rod of length L. The temperature of the rod at a point x (where x is between 0 and L) is given by u(x, t). That is, the temperature changes both along the rod, and with time! A physical model for how the temperature of the rod changes with time is the partial differential equation (L ol where is a constant related to the heat conductance of the bar, and is simply a way of saying "the first derivative of u with respect to time." In order to characterize the behavior, we need both boundary conditions and an initial condition For this problem, we assume the ends of the rod are held at a constant zero temperature. Mathematically, this translates to u(0, t)-0 for all time and u(L,t) 0 for all time. Think of it as if the ends of the rod are sitting in ice baths that are kept at a constant temperature, due to the constantly melting ice Finally, we need to have an initial condition. That is, we need to know what the temperature of the rod is everywhere along it at the starting time! Obviously, the ends are at zero, as they always are, but the initial tempera- ture of the interior points must be provided as an initial function of x (x) Thus, u(z,0) = (z) for all z. Putting all of this together gives us the full problem statement of the heat equation