MATLAB

Write a Matlab script and post the script and the results.

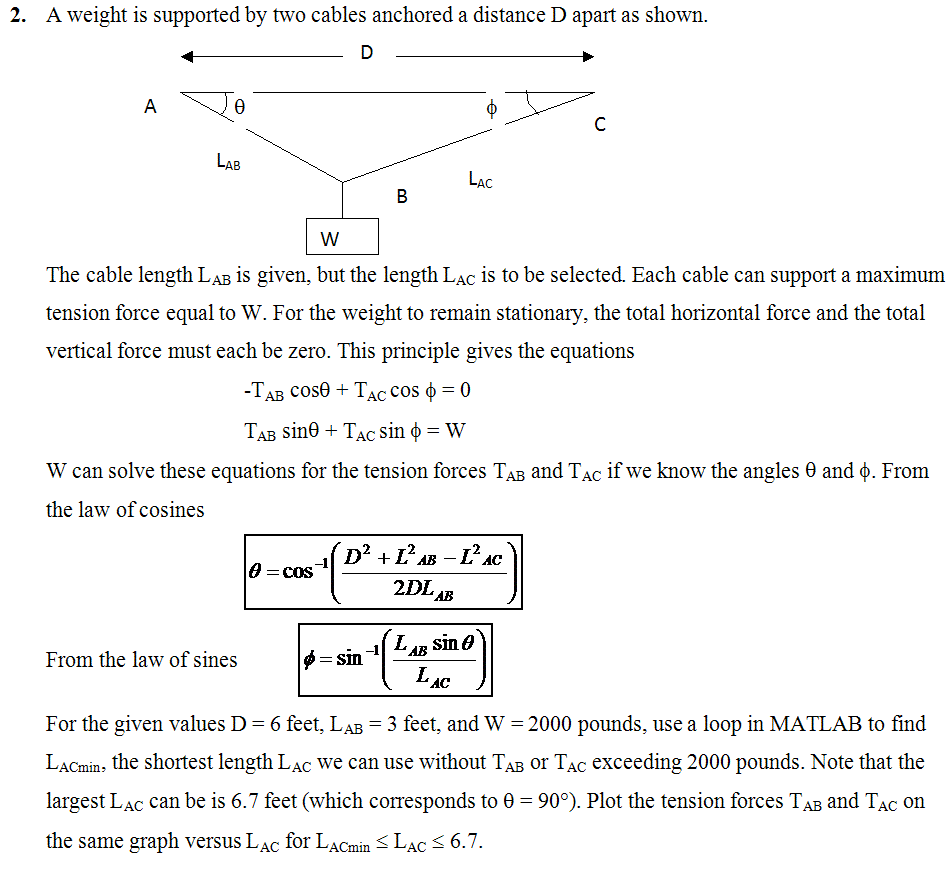
A Weight is supported by two cables anchored a distance D apart as shown. The cable length L_AB is given, but the length L_AC is to be selected. Each cable can support a maximum tension force equal to W. For the weight to remain stationary, the total horizontal force and the total vertical force must each be zero. This principle gives the equations -T_ab cos theta + T_ac cos phi = 0 T_ab sin theta + T_ac sin phi = W W can solve these equations for the tension forces T_AB and T_AC if we know the angles theta and phi. From the law of cosines theta = cos^-1(D^2 + L^2 _AB - L^2 _AC/2DL_AB) From the law of sines phi = sin^-1 (L_AB sin theta/L_AC) For the given values D = 6 feet. L_AB = 3 feet, and W = 2000 pounds, use a loop in MATLAB to find L_ACmin, the shortest length L_AC we can use without T_AB or T_AC exceeding 2000 pounds. Note that the largest L_AC can be is 6.7 feet (which corresponds to theta = 90 degree). Plot the tension forces T_AB and T_AC on the same graph versus L_AC for L_ACmin lessthanorequalto L_AC lessthanorequalto 6.7. A Weight is supported by two cables anchored a distance D apart as shown. The cable length L_AB is given, but the length L_AC is to be selected. Each cable can support a maximum tension force equal to W. For the weight to remain stationary, the total horizontal force and the total vertical force must each be zero. This principle gives the equations -T_ab cos theta + T_ac cos phi = 0 T_ab sin theta + T_ac sin phi = W W can solve these equations for the tension forces T_AB and T_AC if we know the angles theta and phi. From the law of cosines theta = cos^-1(D^2 + L^2 _AB - L^2 _AC/2DL_AB) From the law of sines phi = sin^-1 (L_AB sin theta/L_AC) For the given values D = 6 feet. L_AB = 3 feet, and W = 2000 pounds, use a loop in MATLAB to find L_ACmin, the shortest length L_AC we can use without T_AB or T_AC exceeding 2000 pounds. Note that the largest L_AC can be is 6.7 feet (which corresponds to theta = 90 degree). Plot the tension forces T_AB and T_AC on the same graph versus L_AC for L_ACmin lessthanorequalto L_AC lessthanorequalto 6.7