Part 1

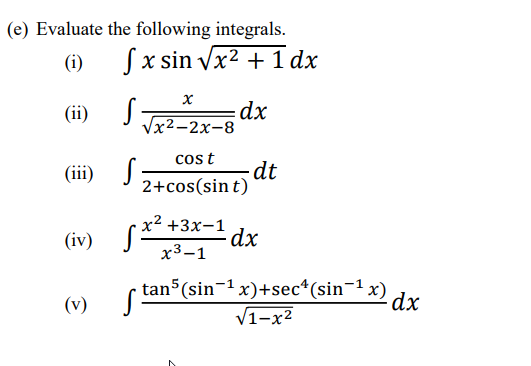
(a) Use n. = 6 subdivisions to approximate the value of E.- va+3dx u by the trapezoidal rule. (b) Find a value for n to ensure that the absolute error in approximating the integral 3 fxsin x 031* a by the midpoint rule will be less than 10". (e) Evaluate 4 -1 (x 2)?dx 1 (d) Solve the differential equation xy' = (1 + 3x3) tan 3;. (e) Evaluate the following integrals. (i) [ x sin Vx2 + 1 dx X (ii) dx Vx2-2x-8 cost (ii) dt 2+cos(sint) x-+3x-1 (iv) dx 73-1 (v ) tan'(sin 1 x)+sec*(sin 1 x) dx V1-x241:. 4\"\" . } 1s 2n+3 (i) increasing or decreasing; {ii} monotone; {iii} bounded and {iv} convergent. (a) Determine whether the sequence { n= 1 (b) Use the divergent test to show that the series +oo En+1 n n=1 diverges. (c) Use the indicated convergence test to determine if the series is convergent or divergent. +60 \"+1 (i) \":1 F Integral Test {ii} .131 5:3 Ratio Test (d) Find the interval of convergence and radius of convergence of the power series \"0 s