Please refer to this first part of code to code for the question:

class DFSTimeCounter:

def $\_\_$init$\_\_($self$)$:

self.count $=0$

def reset$($self$)$:

self.count $=0$

def increment$($self$)$:

self.count $=$ self.count $+1$

def get$($self$)$:

return self.count

class UndirectedGraph:

# n is the number of vertices

# we will label the vertices from $0$ to self.n $-1$

# Initialize to an empty adjacency list

# We will store the outgoing edges using a set data structure

def $\_\_$init$\_\_($self$,$ n$)$:

self.n $=$ n

self.adj$\_$list $=[$ set$()$ for i in range$($self$.$n$)]$

def add$\_$edge$($self$,$ i$,$ j$)$:

assert i $$ self.n

assert j $$ self.n

assert i $!=$ j

# Make sure to add edge from i to j

self.adj$\_$list$[$i$].$add$($j$)$

# Also add edge from j to i

self.adj$\_$list$[$j$].$add$($i$)$

# get a set of all vertices that

# are neighbors of the

# vertex i

def get$\_$neighboring$\_$vertices$($self$,$ i$)$:

assert i $$ self.n

return self.adj$\_$list$[$i$]$

# Function: dfs$\_$visit

# Program a DFS visit of a graph.

# We maintain a list of discovery times and finish times.

# Initially all discovery times and finish times are set to None.

# When a vertex is first visited, we will set discovery time

# When DFS visit has processed all the neighbors then

# set the finish time.

# DFS visit should update the list of discovery and finish times in$-$place

# Arguments

# i $-->$ id of the vertex being visited.

# dfs$\_$timer $-->$ An instance of DFSTimeCounter structure provided for you.

# discovery $-->$ discovery time of each vertex $--$ a list of size self.n

# None if the vertex is yet to be visited.

# finish $-->$ finish time of each vertex $--$ a list of size self.n

# None if the vertex is yet to be finished.

# dfs$\_$tree$\_$parent $-->$ the parent for for each node

# if we visited node j from node i$,$ then j$\text{'}$s parent is i$.$

# Do not forget to set tree$\_$parent when you call dfs$\_$visit

# on node j from node i$.$

# dfs$\_$back$\_$edges $-->$ a list of back edges.

# a back edge is an edge from i to j wherein

# DFS has already discovered j when i is discovered

# but not finished j

def dfs$\_$visit$($self$,$ i$,$ dfs$\_$timer, discovery$\_$times, finish$\_$times,

dfs$\_$tree$\_$parent, dfs$\_$back$\_$edges$)$:

assert i $$ self.n

assert discovery$\_$times$[$i$]==$ None

assert finish$\_$times$[$i$]==$ None

discovery$\_$times$[$i$]=$ dfs$\_$timer.get$()$

dfs$\_$timer.increment$()$

# your code here

for v in self.get$\_$neighboring$\_$vertices$($i$)$:

if discovery$\_$times$[$v$]$ is not None and finish$\_$times$[$v$]$ is None:

dfs$\_$back$\_$edges.append$(($i$,$v$))$

if discovery$\_$times$[$v$]$ is None:

dfs$\_$tree$\_$parent$[$v$]=$ i

self.dfs$\_$visit$($v$,$ dfs$\_$timer, discovery$\_$times, finish$\_$times, dfs$\_$tree$\_$parent, dfs$\_$back$\_$edges$)$

finish$\_$times$[$i$]=$ dfs$\_$timer.get$()$

dfs$\_$timer.increment$()$

# Function: dfs$\_$traverse$\_$graph

# Traverse the entire graph.

def dfs$\_$traverse$\_$graph$($self$)$:

dfs$\_$timer $=$ DFSTimeCounter$()$

discovery$\_$times $=[$None$]*$self$.$n

finish$\_$times $=[$None$]*$self$.$n

dfs$\_$tree$\_$parents $=[$None$]*$self$.$n

dfs$\_$back$\_$edges $=[]$

for i in range$($self$.$n$)$:

if discovery$\_$times$[$i$]==$ None:

self.dfs$\_$visit$($i$,$dfs$\_$timer, discovery$\_$times, finish$\_$times,

dfs$\_$tree$\_$parents, dfs$\_$back$\_$edges$)$

# Clean up the back edges so that if $($i$,$j$)$ is a back edge then j cannot

# be i$\text{'}$s parent.

non$\_$trivial$\_$back$\_$edges $=[($i$,$j$)$ for $($i$,$j$)$ in dfs$\_$back$\_$edges if dfs$\_$tree$\_$parents$[$i$]!=$ j$]$

return $($dfs$\_$tree$\_$parents, non$\_$trivial$\_$back$\_$edges, discovery$\_$times, finish$\_$times$)$

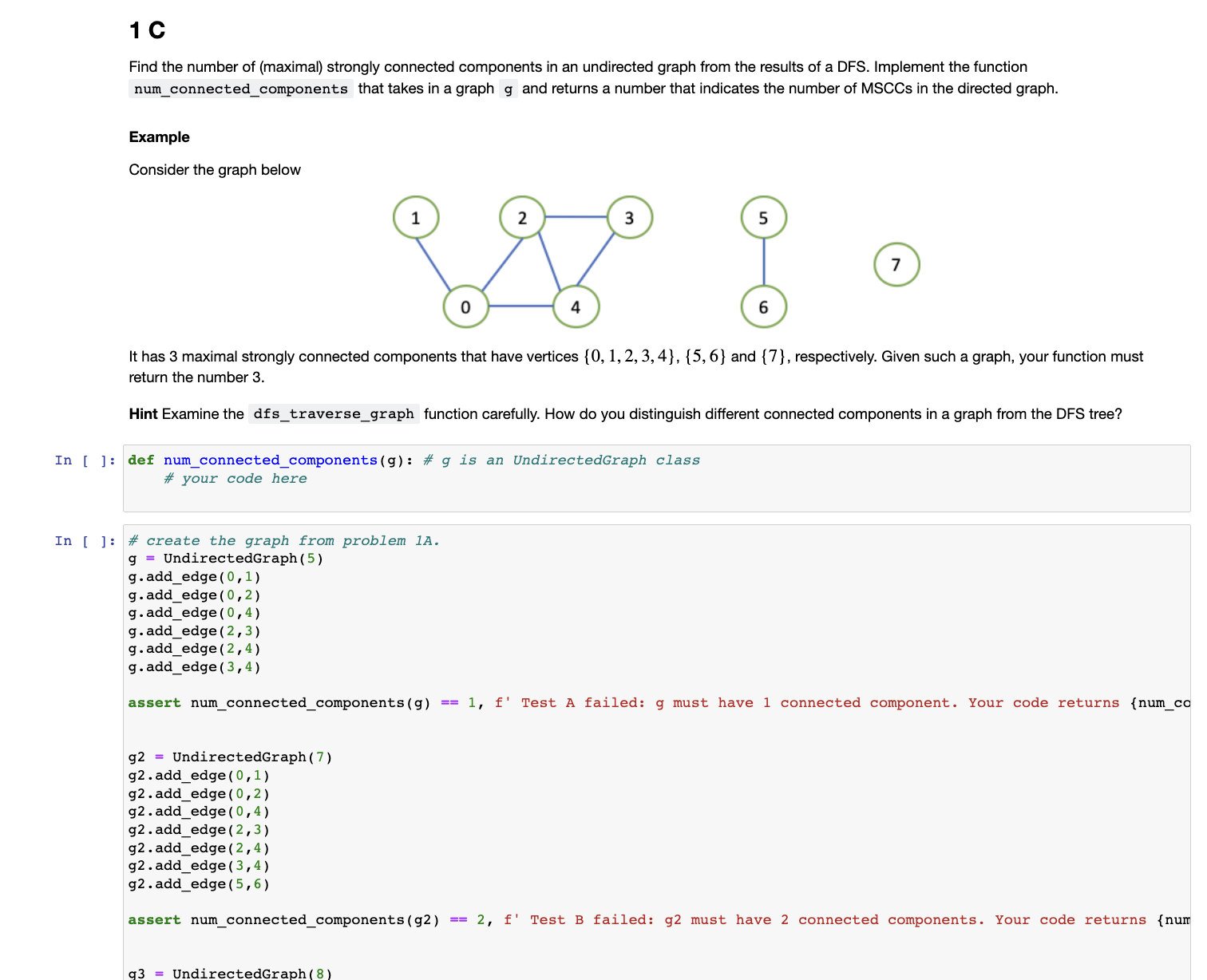
The second question is in the image.Find the number of $($maximal$)$ strongly connected components in an undirected graph from the results of a DFS$.$ Implement the function

num$\_$connected$\_$components that takes in a graph g and returns a number that indicates the number of MSCCs in the directed graph.

Example

Consider the graph below

It has $3$ maximal strongly connected components that have vertices $\{0,1,2,3,4\},\{5,6\}$ and $\{7\},$ respectively. Given such a graph, your function must

return the number $3.$

Hint Examine the dfs$\_$traverse$\_$graph function carefully. How do you distinguish different connected components in a graph from the DFS tree?

In $[]$: def num$\_$connected$\_$components$($g$)$: # g is an UndirectedGraph classIn $[]$: # create the graph from problem $1$A$.$

g $=$ UndirectedGraph$(5)$

g$.$add$\_$edge $(0,1)$

g$.$add$\_$edge $(0,2)$