Please solve below by following these steps:

In summary, here are the steps for solving an initial value problem with the Laplace transform. The Laplace table is given as the last page of this worksheet.

1. Take the Laplace transform of both sides of the equation.

2. Plug in the initial conditions and solve the new equation for Y psq ? L typtqu.

3. Take the inverse Laplace transform of both sides. You may need to use partial fraction decomposition before you can take the inverse transform.

4. This function y(t) is the solution to the original IVP.

Make sure you take the inverse Laplace transform please

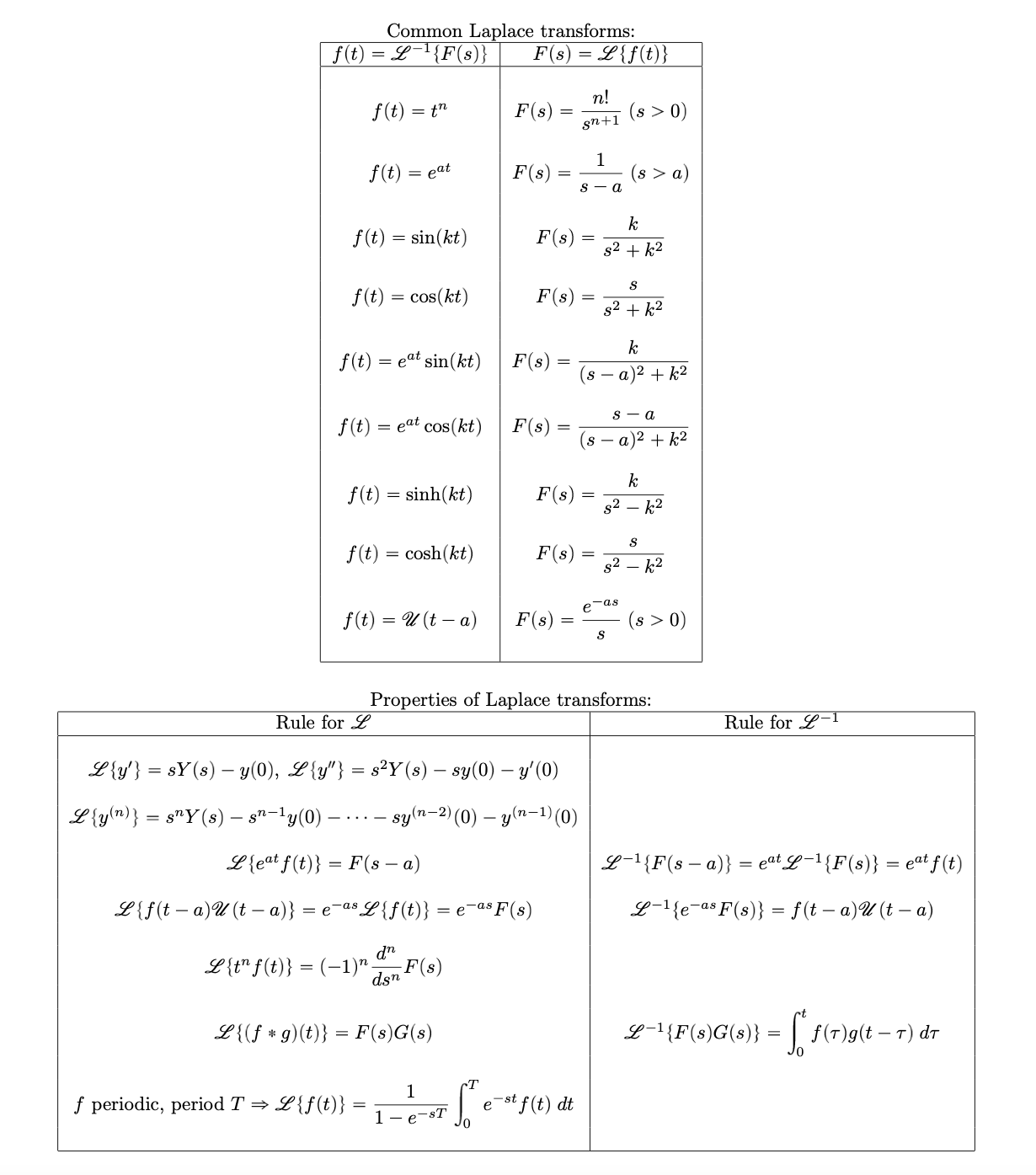
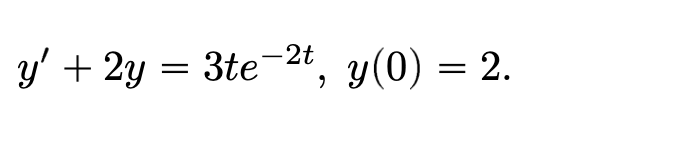
Common Laplace transforms: f (t) = 2-1{F(s) } F(s) = Lif(t) } f (t) = tn F(s) = n! anti ($ > 0) f (t) = eat F(s) = - s - a (s > a) k f (t) = sin(kt) F( s) = - $ 2 + K 2 S f (t) = cos(kt) F (s) = - $2 + K2 k f (t) = eat sin(kt) F(s) = 7 (s - a) 2+ k2 f (t) = eat cos(kt) F(s) = - s - a (s - a) 2+k2 k f (t) = sinh(kt) F(s) = $2 - K 2 S f (t) = cosh(kt) F(s) = $2 - 12 f (t) = 2(t - a) F(s) = e-as S - (s > 0) Properties of Laplace transforms: Rule for L Rule for 2-1 Lly') = sY(s) - y(0), Lly") = say(s) - sy(0) - y'(0) Lly'n) } = sny(s) - sn-ly(0) - ... - sy(n-2)(0) - y(n-1)(0) Lleat f (t) } = F(s - a) 2-1 (F (s - a)} = eat 2-1 (F(s) ) = eat f(t) Lif (t - a)2 (t - a)} = e-as Lif (t) ) = e-asF(s) 2-1 (e - as F (s ) } = f (t - a)U (t -a) eith f (t ) ) = ( - 1 )n d' dan F(s) LI (f * g ) (t) } = F(s)G(s) 2-1 ( F (s) G (s ) ) = f (T)g (t - T ) dr f periodic, period T = Lif(t)} = 1 - e-ST e- st f ( t ) dt\f