please use solver to solve

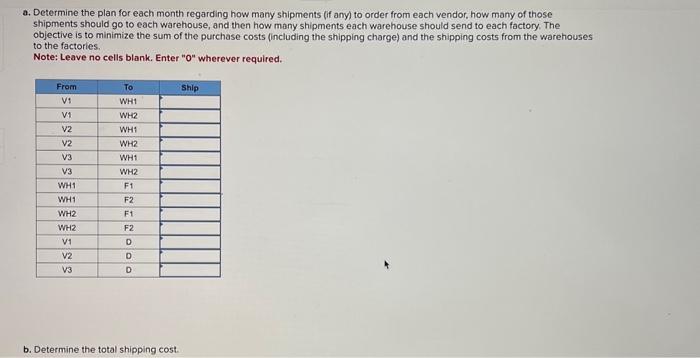
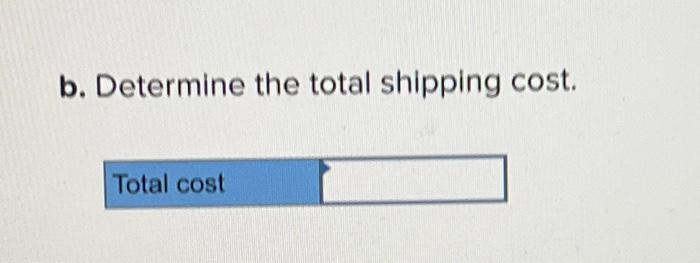
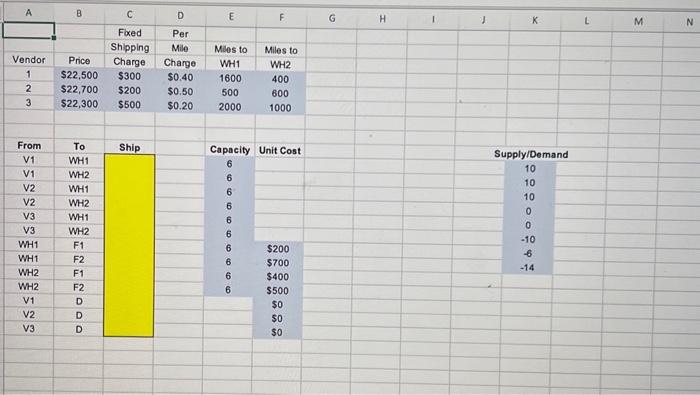
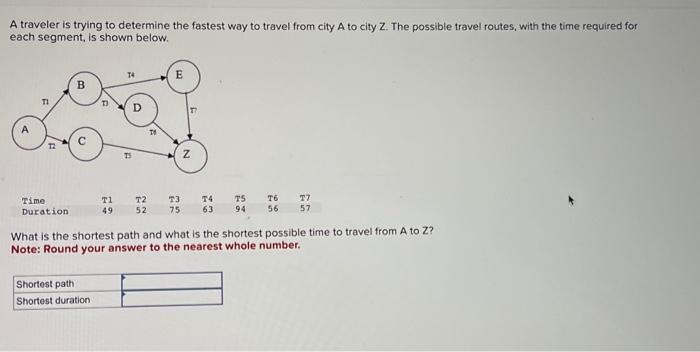
\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline A & B & C & D & E & F & G & H & 1 & J & K & L & M & N \\ \hline & & Foxed & Per & & & & & & & & & & \\ \hline & & Shipping & Mile & Milos to & Miles to & & & & & & & & \\ \hline Vendor & Price & Charge & Charge & WH1 & WH2 & & & & & & & & \\ \hline 1 & $22,500 & $300 & $0.40 & 1600 & 400 & & & & & & & & \\ \hline 2 & $22,700 & $200 & $0.50 & 500 & 600 & & & & & & & & \\ \hline 3 & $22,300 & $500 & $0.20 & 2000 & 1000 & & & & & & & & \\ \hline & & & & & & & & & & & & & \\ \hline & & & & & & & " & & & & & & \\ \hline From & To & Ship & & Capacity & Unit Cost & & & & \multicolumn{3}{|c|}{ Supply/Demand } & & \\ \hline V1 & WH1 & & & 6 & & & & & & 10 & & & \\ \hline V1 & WH2 & & & 6 & & & & & & 10 & & & \\ \hline V2 & WH1 & & & 6 & & & & & & 10 & & & \\ \hline V2 & WH2 & & & 6 & & & & & & 0 & & & \\ \hline v3 & WH1 & & & 6 & & & & & & 0 & & & \\ \hline V3 & WH2 & & & 6 & & & & & & -10 & & & \\ \hline WH1 & F1 & & & 6 & $200 & & & & & -6 & & & \\ \hline WH1 & F2 & & & 6 & $700 & & & & & -14 & & & \\ \hline WH2 & F1 & & & 6 & $400 & & & & & & & & \\ \hline WH2 & F2 & & & 6 & $500 & & & & & & & & \\ \hline V1 & D & & & & $0 & & & & & & & & \\ \hlinev2 & D & & & & $0 & & & & & & & & \\ \hline V3 & D & & & & $0 & & & & & & & & \\ \hline & & & & & & & & & & & & & \\ \hline & & & & & & & & & & & & & \\ \hline & & & & & & & & & & & & & \\ \hline \end{tabular} A traveler is trying to determine the fastest way to travel from city A to city Z. The possible travel routes, with the time required for each segment, is shown below. What is the shortest path and what is the shortest possible time to travel from A to Z ? Note: Round your answer to the nearest whole number. The Audiofile Company produces boomboxes. However, management has decided to subcontract out the production of the speakers needed for the boomboxes. Three vendors are avallable to supply the speakers. Their price for each shipment of 1,000 speakers is shown below. Each shipment would go to one of the company's two warehouses. In addition to the price for each shipment, each vendor would charge a shipping cost for which it has its own formula based on the mileage to the warehouse. These formulas and the mileage data are shown below. Whenever one of the company's two factories needs a shipment of speakers to assemble into the boomboxes, the company hires a trucker to bring the shipment in from one of the warehouses. The cost per shipment is given next, along with the number of shipments needed per month at each factory. Each vendor is able to supply as many as 10 shipments per month. However, because of shipping limitations, each vendor is only able to send a maximum of six shipments per month to each warehouse. Similarly, each warehouse is only able to send a maximum of six shipments per month to each factory. Click here for the Excel Data File b. Determine the total shipping cost. a. Determine the plan for each month regarding how many shipments (if any) to order from each vendor, how many of those shipments should go to each warehouse, and then how many shipments each warehouse should send to each factory. The objective is to minimize the sum of the purchase costs (including the shipping charge) and the shipping costs from the warehouses to the factorles. Note: Leave no cells blank. Enter " 0 " wherever required. b. Determine the total shipping cost