Problem $1$: $(10\backslash \%$ of Assignment Value$)$

To find the self$-$inductance of a coil, we write the EMF through the coil two ways; first, using the basic relation for self$-$inductance and second, using Faraday's law:

$\backslash [$

$\backslash$mathcal$\{$E$\}\_\{$L$\}=-$L $\backslash$frac$\{$d I$\}\{$d t$\}=-$N $\backslash$frac$\{$d $\backslash$Phi$\_\{$B $1\}\}\{$d t$\}$

$\backslash ]$

Therefore the self$-$inductance of the coil is

$\backslash [$

L$=\backslash$frac$\{$N $\backslash$Phi$\_\{$B $1\}\}\{$I$\}$

$\backslash ]$

Here $\backslash ($ L $\backslash )$ is the self$-$inductance, $\backslash ($ I $\backslash )$ is the current through the inductor, $\backslash ($ N $\backslash )$ is the number of turns in the inductor, and $\backslash (\backslash$Phi$\_\{$B $1\}\backslash )$ is the magnetic flux through one turn of the inductor.

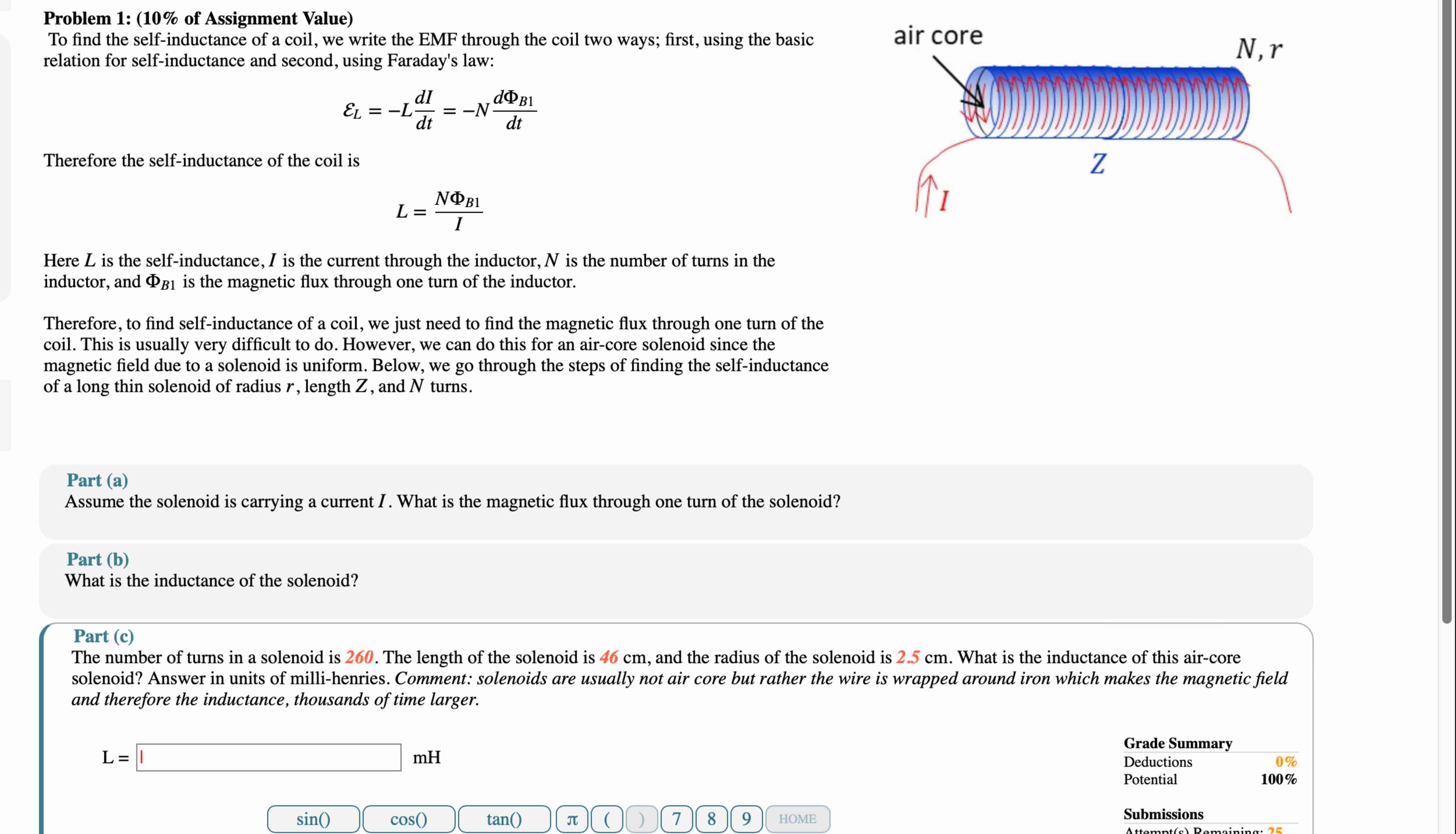
Therefore, to find self$-$inductance of a coil, we just need to find the magnetic flux through one turn of the coil. This is usually very difficult to do$.$ However, we can do this for an air$-$core solenoid since the magnetic field due to a solenoid is uniform. Below, we go through the steps of finding the self$-$inductance of a long thin solenoid of radius $\backslash ($ r $\backslash ),$ length $\backslash ($ Z $\backslash ),$ and $\backslash ($ N $\backslash )$ turns.

Part $($a$)$

Assume the solenoid is carrying a current $\backslash ($ I $\backslash ).$ What is the magnetic flux through one turn of the solenoid?

Part $($b$)$

What is the inductance of the solenoid?

Part $($c$)$

The number of turns in a solenoid is $260.$ The length of the solenoid is $46$ cm $,$ and the radius of the solenoid is $2\mathrm{.}5$ cm $.$ What is the inductance of this air$-$core solenoid? Answer in units of milli$-$henries. Comment: solenoids are usually not air core but rather the wire is wrapped around iron which makes the magnetic field and therefore the inductance, thousands of time larger.

$\backslash [$

$\backslash$mathrm$\{$L$\}=\backslash$quad $\backslash$mathrm$\{$mH$\}$

$\backslash ]$

Submissions