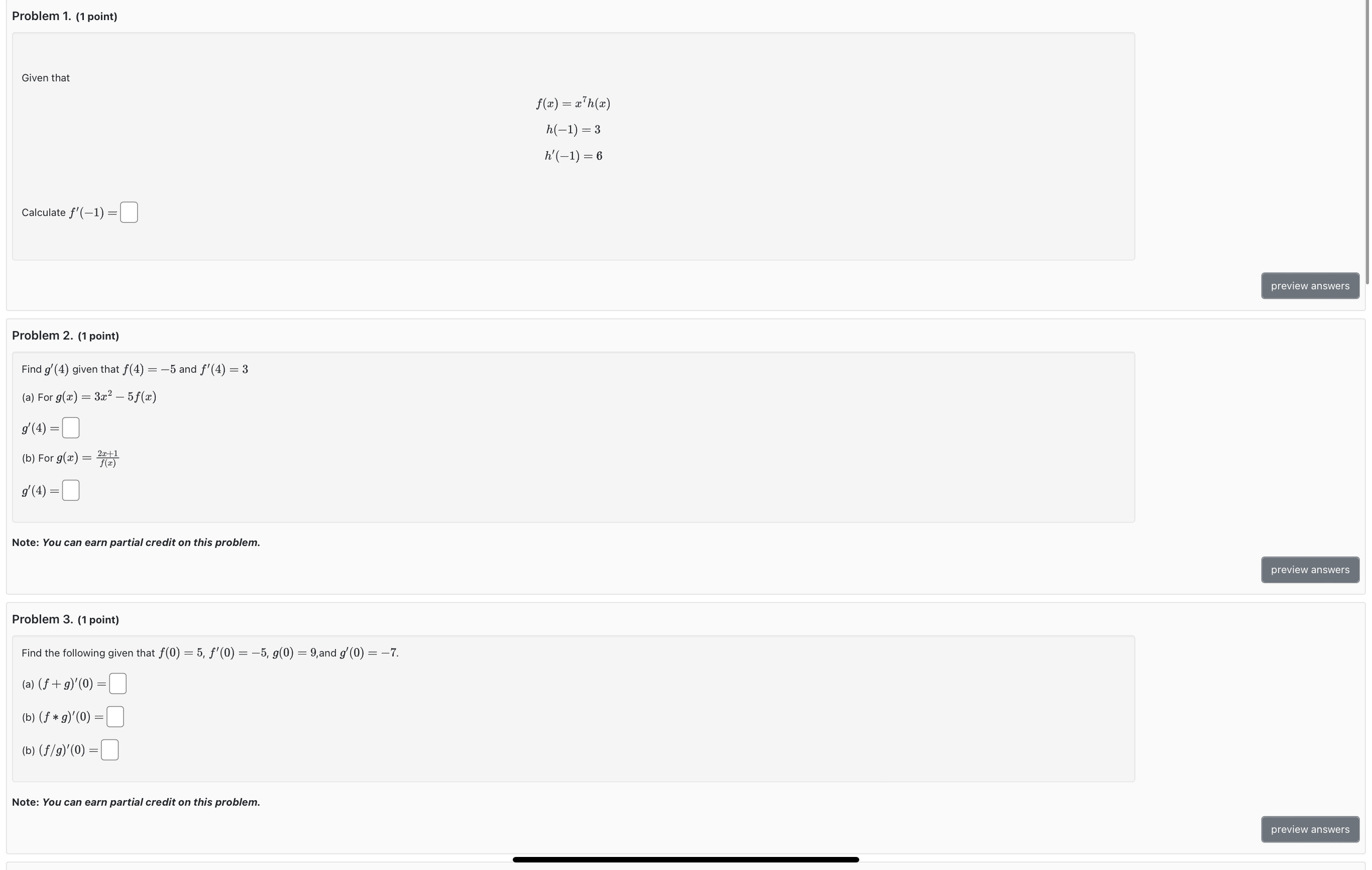
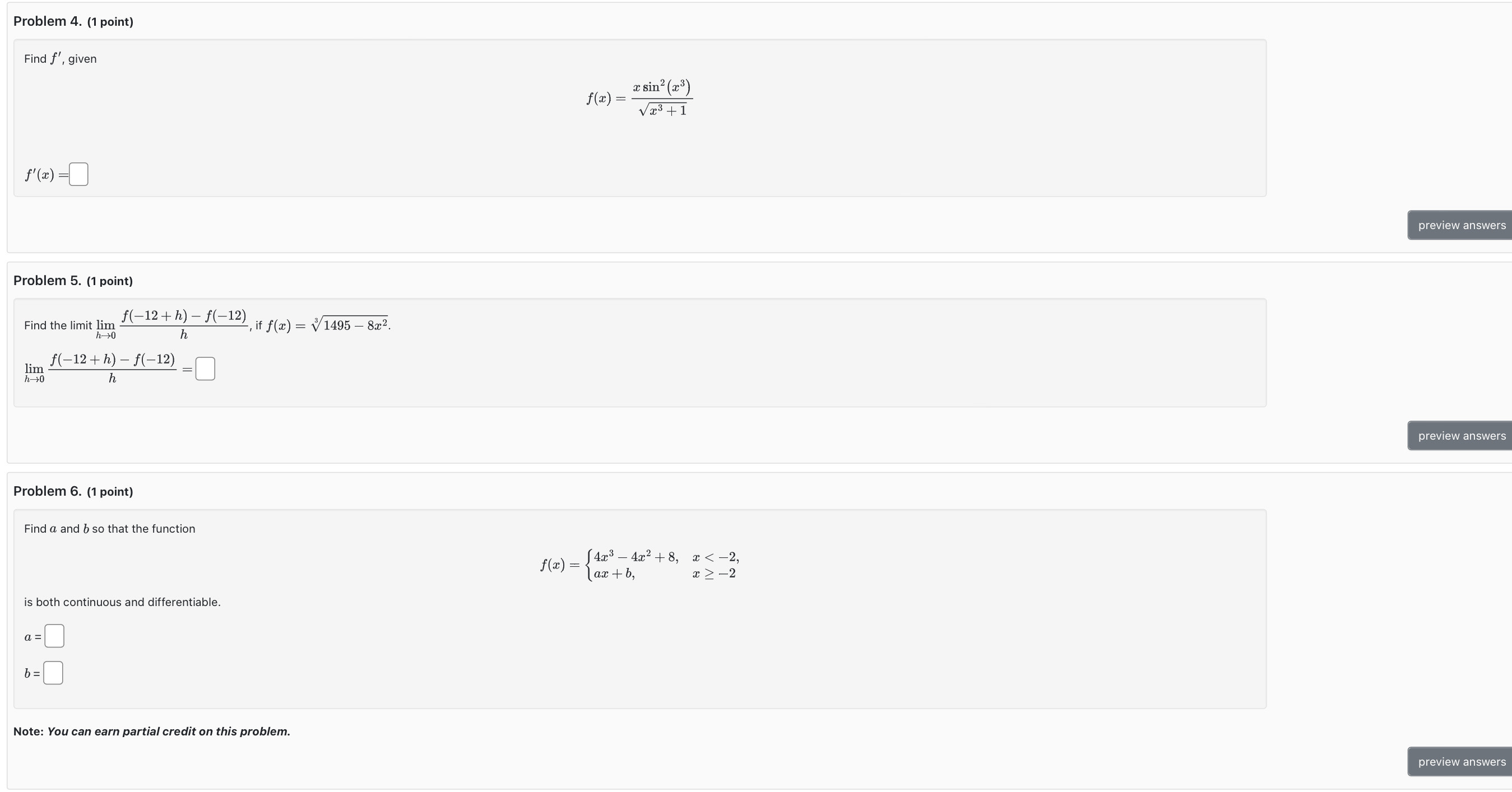
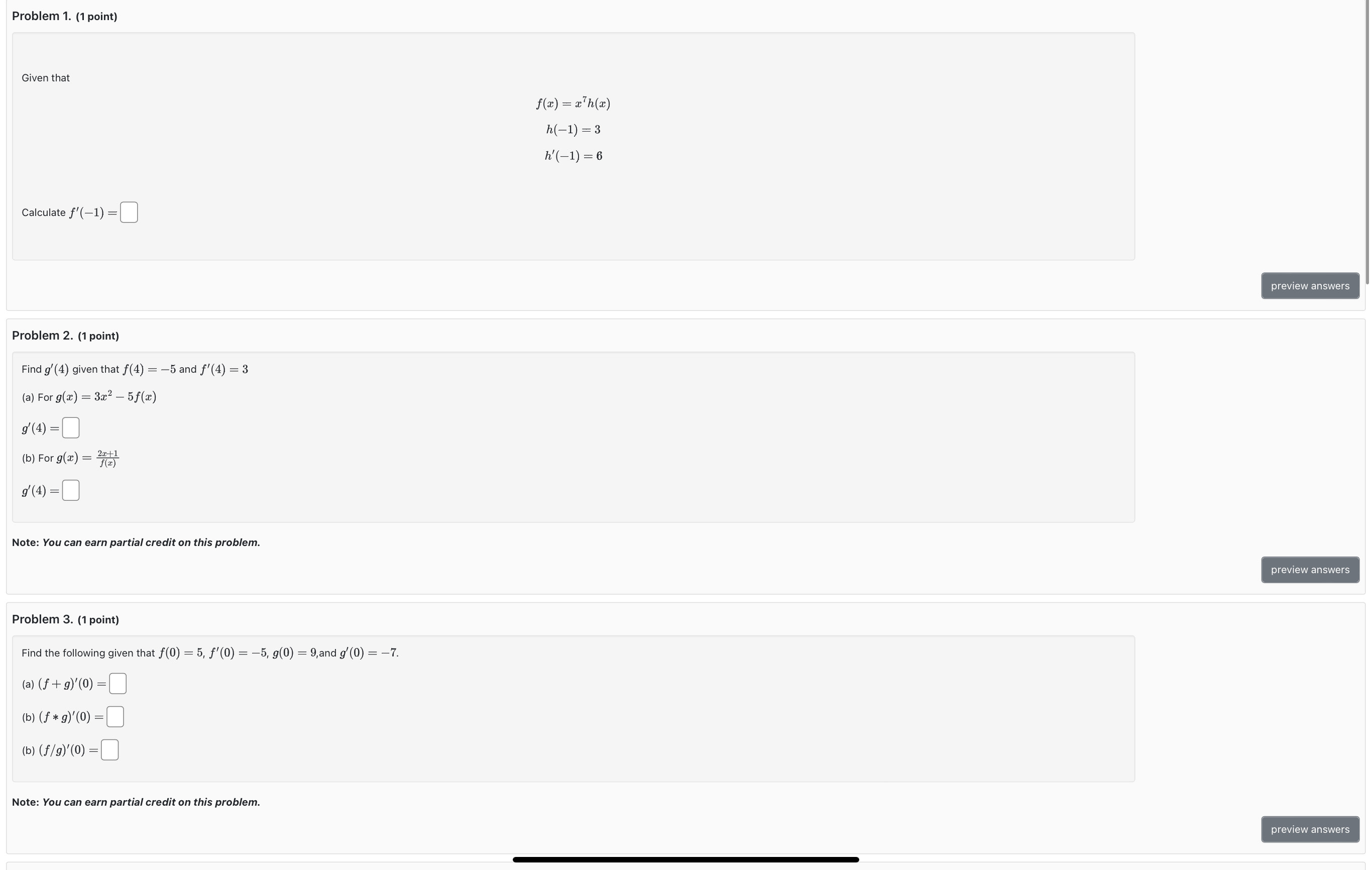
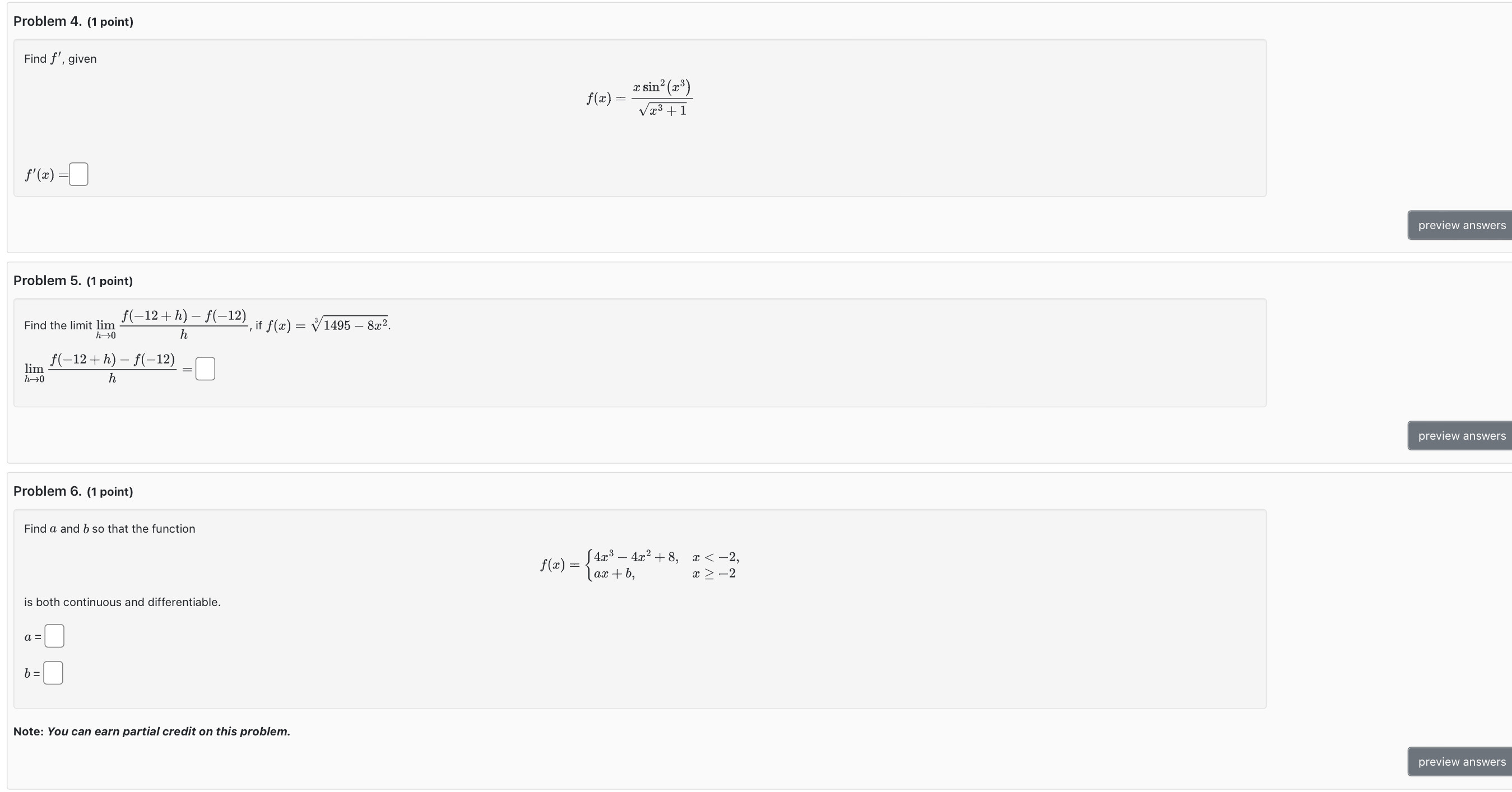
Problem 1. (1 point) Given that f(z) = a h(z) h(-1) = 3 h' ( -1) = 6 Calculate f'(-1) = preview answers Problem 2. (1 point) Find g'(4) given that f(4) = -5 and f'(4) = 3 (a) For g(x) = 3x2 - 5f(x) 9'(4) =0 (b) For g(2) = 241 9'(4) =0 Note: You can earn partial credit on this problem. preview answers Problem 3. (1 point) Find the following given that f(0) = 5, f'(0) = -5, g(0) = 9,and g'(0) = -7. (a) (f + 9)'(0) =[ (b) (f * 9)' (0 ) = 1 ( b ) ( f / g )' ( 0 ) = [ Note: You can earn partial credit on this problem. preview answersProblem 4. (1 point) Find f , given x sin (23) f(2) = Vx3 +1 f' ( 2 ) =0 preview answers Problem 5. (1 point) Find the limit lim f(-12 + h) - f(-12) if f(x) = 1495 - 82. h lim f(-12 + h) - f(-12) h -+0 0 preview answers Problem 6. (1 point) Find a and b so that the function f(2) = 425 - 4x2 +8, 2