Question: Problem 1 . Laplace Transforms ( 2 0 points ) The diagram shows an inverted pendulum on a cart that is driven by an external
Problem Laplace Transforms
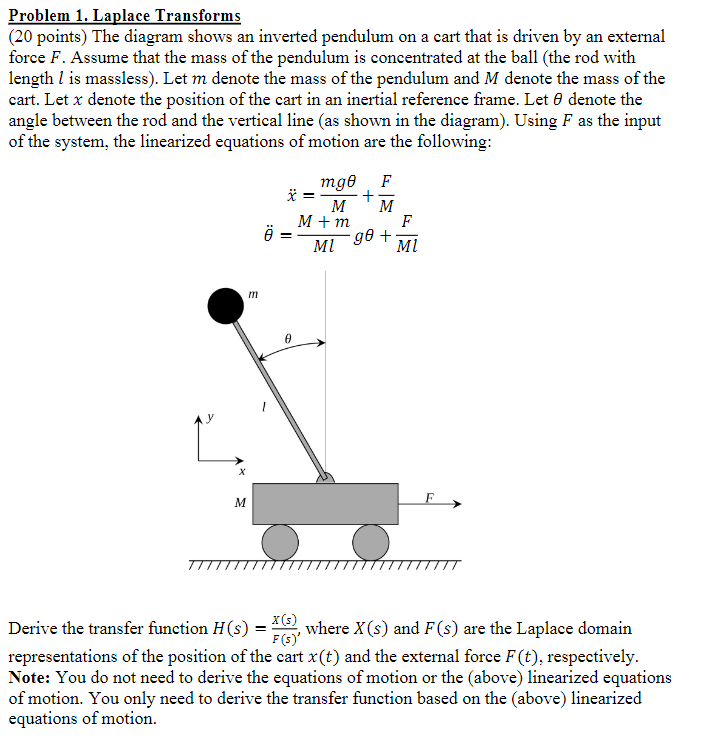
points The diagram shows an inverted pendulum on a cart that is driven by an external
force Assume that the mass of the pendulum is concentrated at the ball the rod with
length is massless Let denote the mass of the pendulum and denote the mass of the
cart. Let denote the position of the cart in an inertial reference frame. Let denote the
angle between the rod and the vertical line as shown in the diagram Using as the input
of the system, the linearized equations of motion are the following:
Derive the transfer function where and are the Laplace domain
representations of the position of the cart and the external force respectively.
Note: You do not need to derive the equations of motion or the above linearized equations
of motion. You only need to derive the transfer function based on the above linearized
equations of motion.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


