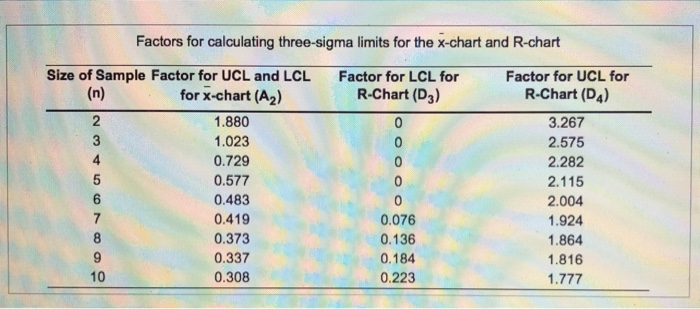
Question: Problem 20 An automatic lathe produces rollers for roller bearings, and the process is monitored by statistical process control charts. The central line of the

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


