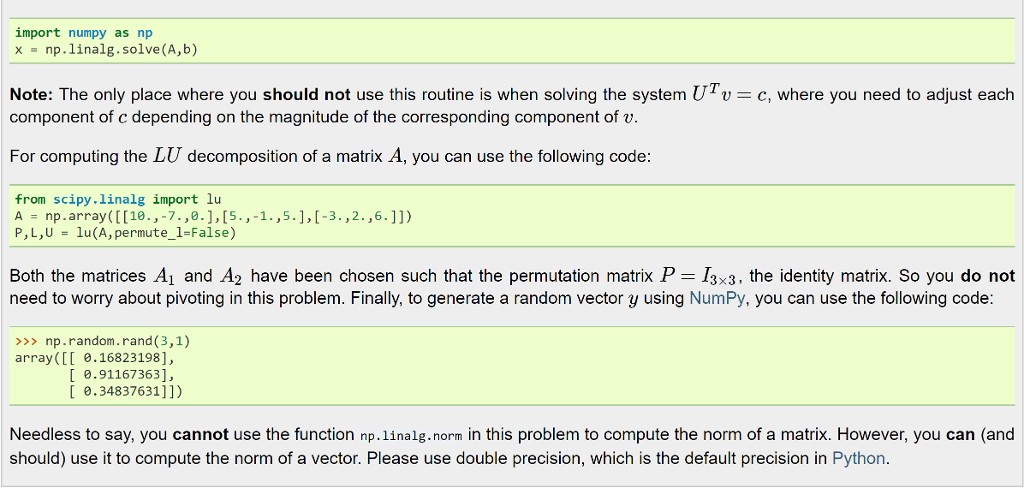
Problem Write a routine for estimating the condition number (A) of a matrix A using the L1-norm. You will need to compute |Al, which should be easy, and estimate |A11, which is more challenging. Note that we only want to estimate |A-1l1, not compute it exactly (up to finite precision). One way to estimate IA-i | i is to choose a vector y such that the ratio 11/llyll is large, where z is the solution to Azy. Try two different approaches to choosing y: a. Choose y as the solution to the system Ary = c, where c is a vector each of whose components is 1 , with the sign for each component chosen by the following heuristic. Using the factorization A-LU, the system ATy c is solved in two stages, successively solving the triangular systems Uc and L'y-v. At each step of the first triangular solution, choose the corresponding component of c to be either 1 or -1, depending on which will make the resulting component of v larger in magnitude. (You will need to write a custom triangular solution routine to implement this.) Then solve the second triangular system in the usual way for y. The idea here is that any ill-conditioning in A will be reflected in U, resulting in a relatively large v. The relatively well- conditioned unit triangular matrix IZ will then preserve this relationship, resulting in a relatively large y. b. Choose five different vectors y randomly and use the one producing the largest ratio /ly!' Test both the approaches described in parts (a) and (b) on each of the following two matrices: Problem Write a routine for estimating the condition number (A) of a matrix A using the L1-norm. You will need to compute |Al, which should be easy, and estimate |A11, which is more challenging. Note that we only want to estimate |A-1l1, not compute it exactly (up to finite precision). One way to estimate IA-i | i is to choose a vector y such that the ratio 11/llyll is large, where z is the solution to Azy. Try two different approaches to choosing y: a. Choose y as the solution to the system Ary = c, where c is a vector each of whose components is 1 , with the sign for each component chosen by the following heuristic. Using the factorization A-LU, the system ATy c is solved in two stages, successively solving the triangular systems Uc and L'y-v. At each step of the first triangular solution, choose the corresponding component of c to be either 1 or -1, depending on which will make the resulting component of v larger in magnitude. (You will need to write a custom triangular solution routine to implement this.) Then solve the second triangular system in the usual way for y. The idea here is that any ill-conditioning in A will be reflected in U, resulting in a relatively large v. The relatively well- conditioned unit triangular matrix IZ will then preserve this relationship, resulting in a relatively large y. b. Choose five different vectors y randomly and use the one producing the largest ratio /ly!' Test both the approaches described in parts (a) and (b) on each of the following two matrices