PYTHON CODE

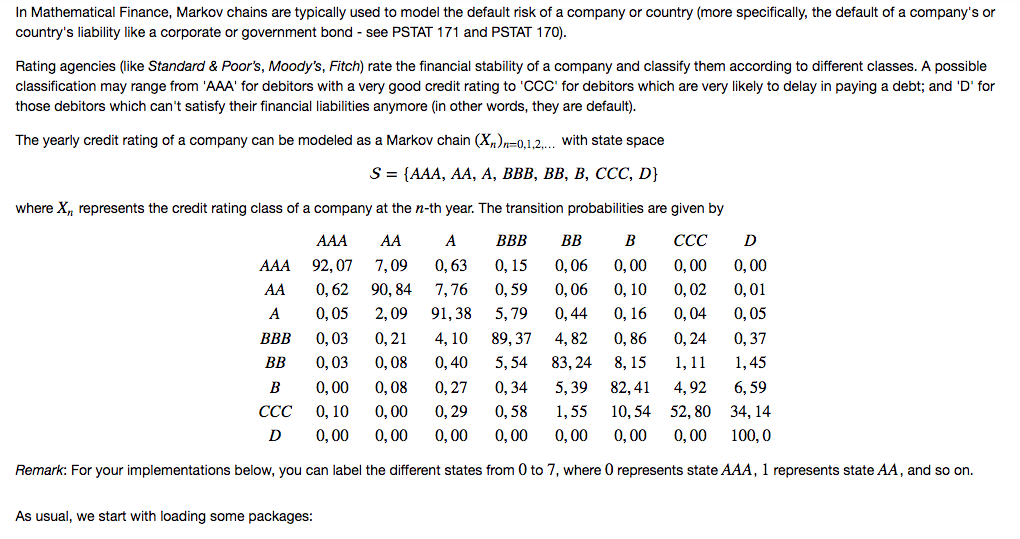
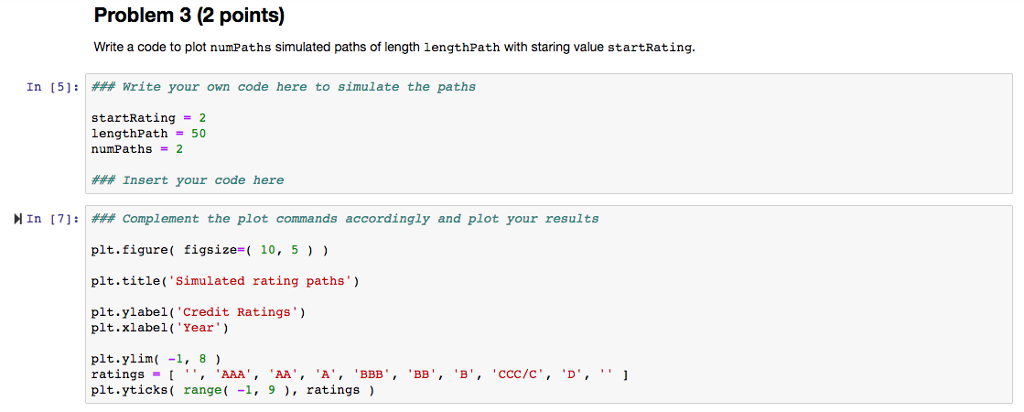
In Mathematical Finance, Markov chains are typically used to model the default risk of a company or country (more specifically, the default of a company's or country's liability like a corporate or government bond - see PSTAT 171 and PSTAT 170). Rating agencies (like Standard & Poor's, Moody's, Fitch) rate the financial stability of a company and classify them according to different classes. A possible classification may range from 'AAA' for debitors with a very good credit rating to 'CCC' for debitors which are very likely to delay in paying a debt; and 'D' for those debitors which can't satisfy their financial liabilities anymore (in other words, they are default) The yearly credit rating of a company can be modeled as a Markov chain (X)-0,1,2. with state space where Xn represents the credit rating class of a company at the n-th year. The transition probabilities are given by AAA 92,07 7,09 0,63 0,15 0,06 0,00 0,00 0,00 AA 0, 62 90,84 7,76 0,59 0, 06 0,10 0,02 0,01 A0,05 2,09 91,38 5,79 0,44 0,16 0,04 0, 05 BBB 0,03 0,21 4,10 89,37 4,82 0,86 0,24 0,37 BB 0,03 0,08 0,40 5,54 83, 24 8, 15 l, l 1,45 0,00 0,08 0,27 0,34 5,39 82, 41 4,92 6,59 ccc 0,10 0,00 0,29 0,58 1,55 10,54 52,80 34,14 D 0,00 0,00 0,00 0,00 0,00 0,00 0,00 100,0 Remark: For your implementations below, you can label the different states from 0 to 7, where 0 represents state AAA, 1 represents state AA, and so on. As usual, we start with loading some packages: In Mathematical Finance, Markov chains are typically used to model the default risk of a company or country (more specifically, the default of a company's or country's liability like a corporate or government bond - see PSTAT 171 and PSTAT 170). Rating agencies (like Standard & Poor's, Moody's, Fitch) rate the financial stability of a company and classify them according to different classes. A possible classification may range from 'AAA' for debitors with a very good credit rating to 'CCC' for debitors which are very likely to delay in paying a debt; and 'D' for those debitors which can't satisfy their financial liabilities anymore (in other words, they are default) The yearly credit rating of a company can be modeled as a Markov chain (X)-0,1,2. with state space where Xn represents the credit rating class of a company at the n-th year. The transition probabilities are given by AAA 92,07 7,09 0,63 0,15 0,06 0,00 0,00 0,00 AA 0, 62 90,84 7,76 0,59 0, 06 0,10 0,02 0,01 A0,05 2,09 91,38 5,79 0,44 0,16 0,04 0, 05 BBB 0,03 0,21 4,10 89,37 4,82 0,86 0,24 0,37 BB 0,03 0,08 0,40 5,54 83, 24 8, 15 l, l 1,45 0,00 0,08 0,27 0,34 5,39 82, 41 4,92 6,59 ccc 0,10 0,00 0,29 0,58 1,55 10,54 52,80 34,14 D 0,00 0,00 0,00 0,00 0,00 0,00 0,00 100,0 Remark: For your implementations below, you can label the different states from 0 to 7, where 0 represents state AAA, 1 represents state AA, and so on. As usual, we start with loading some packages