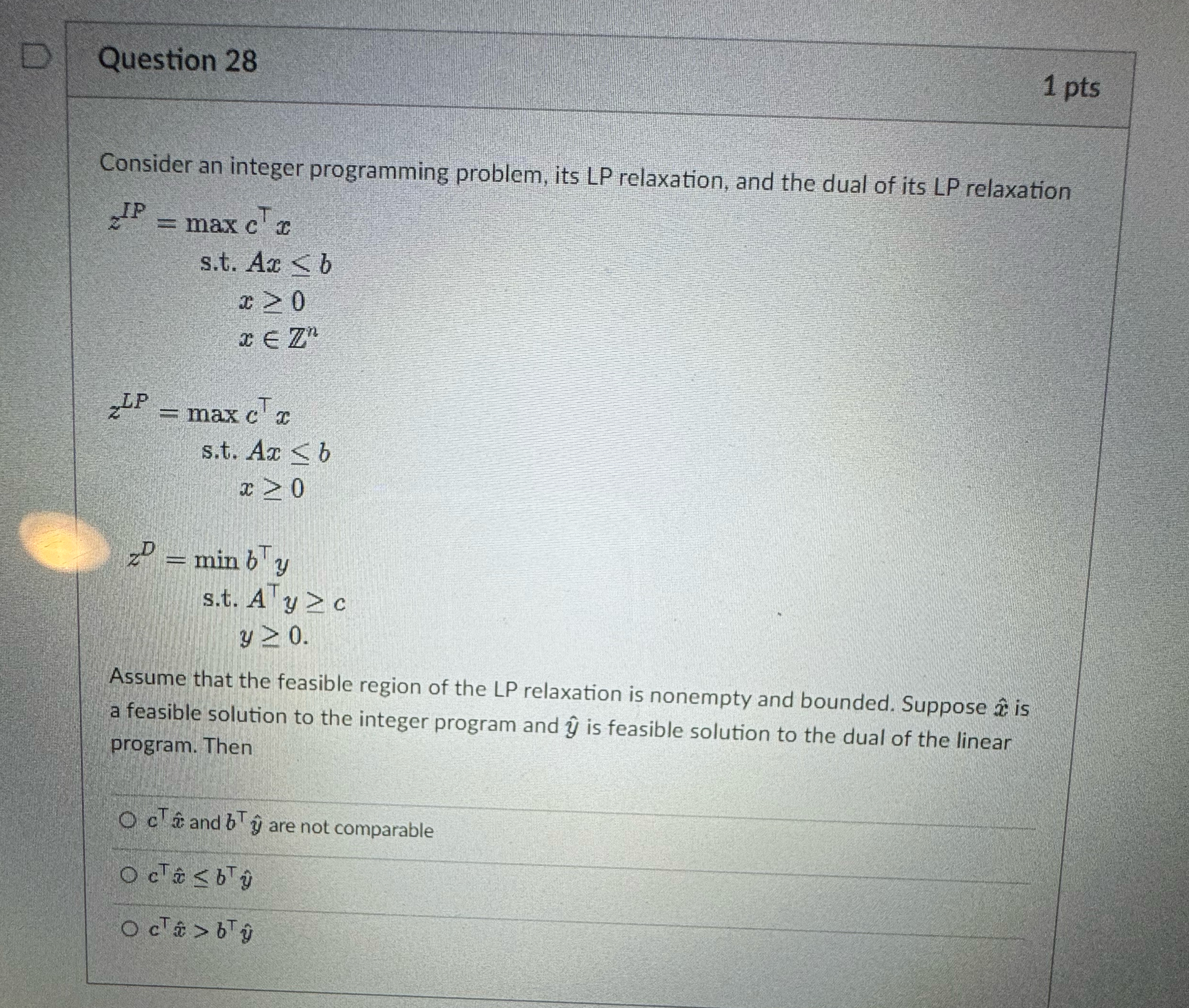
Question $28$

$1$ pts

Consider an integer programming problem, its LP relaxation, and the dual of its LP relaxation

$z^{IP}=max{c}^{TT}x$

$s.t.Axb$

$x0$

$xin{Z}^n$

$z^{LP}=max{c}^{TT}x$

$s.t.Axb$

$x0$

$z^D=min{b}^{TT}y$

$s.t.A^{TT}yc$

$y0$

Assume that the feasible region of the LP relaxation is nonempty and bounded. Suppose hat$(x)$ is a feasible solution to the integer program and hat$(y)$ is feasible solution to the dual of the linear program. Then

$c^{TT}$hat$(x)$ and $b^{TT}$hat$(y)$ are not comparable

$c^{TT}$hat$(x)b^{TT}$hat$(y)$

$c^{TT}$hat$(x)>b^{TT}$hat$(y)$