Question: Refer to Table S6.1 - Factors for Computing Control Chart Limits ( 3 sigma) for this problem. computed. The results were: begin{tabular}{ccc|ccc} hline Sample &

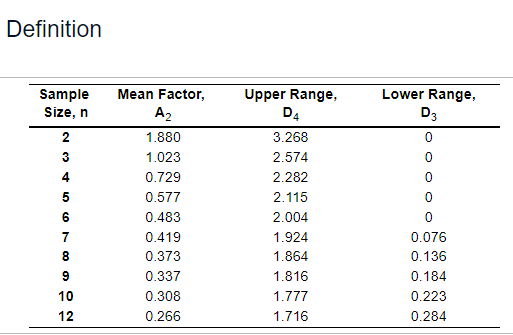
$( 3 sigma) for this problem. computed. The results were: \begin{tabular}{ccc|ccc} \hline$

Sample & SampleMean(in.) & Range (in.) & Sample & Sample Mean (in.)

Refer to Table S6.1 - Factors for Computing Control Chart Limits ( 3 sigma) for this problem. computed. The results were: \begin{tabular}{ccc|ccc} \hline Sample & SampleMean(in.) & Range (in.) & Sample & Sample Mean (in.) Range (in.) \\ \hline 1 & 8.904 & 0.033 & 7 & 8.903 & 0.041 \\ 2 & 8.904 & 0.041 & 8 & 8.907 & 0.034 \\ 3 & 8.889 & 0.034 & 9 & 8.893 & 0.027 \\ 4 & 8.904 & 0.051 & 10 & 8.903 & 0.029 \\ 5 & 8.897 & 0.031 & 11 & 8.901 & 0.039 \\ 6 & 8.899 & 0.036 & 12 & 8.906 & 0.047 \\ \hline \end{tabular} Definition For the given data, the x= inches (round your response to four decimal places). Based on the sampling done, the control limits for 3-sigma x chart are: Upper Control Limit (UCLx)= inches (round your response to four decimal places). Lower Control Limit (LCL)= inches (round your response to four decimal places). Based on the x-chart, is one or more samples beyond the control limits? For the given data, the R= inches (round your response to four decimal places). The control limits for the 3-sigma R-chart are: Upper Control Limit (UCLR)= inches (round your response to four decimal places). Lower Control Limit (LCLR)= inches (round your response to four decimal places). Based on the R-chart, is one or more samples beyond the control limits

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Refer to Table S6.1 - Factors for Computing Control Chart Limits ( 3 sigma) for this problem. computed. The results were: \begin{tabular}{ccc|ccc} \hline Sample & SampleMean(in.) & Range (in.) &...

I need a professional answer to this question I need a professional answer I need a professional answer = Homework: Portfolio 2 Part 3 (chapter 7 & supplement 7) Question 15, Problem S7.18 Part 1 of...

Peter Schromontorit The machte jeta e tento de Corowy The whole or in the samples was determined. There was bad and sample means and rarons were como The Sample for Men 000 05 03 OS Sample sample...

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Thank you so much!! Boxes of Honey-Nut Oatmeal are produced to contain 16.0 ounces, with a standard deviation of 0.10 ounce. For a sample size of 36, the 3-sigma x...

Please provide all formulas/steps if possible Refer to Table S6.1 - Factors for Computing Control Chart Limits (3 sigma) LOADING... for this problem. Twelve samples, each containing five parts, were...

Refer to Table S6.1 - Factors for Computing Control Chart Limits ( 3 sigma) for this problem. computed. The results were: \begin{tabular}{ccc|ccc} \hline Sample & SampleMean(in.) & Range (in.) &...

Sample Size , n Mean Factor, A Subscript 2 Upper Range, D Subscript 4 Lower Range, D Subscript 3 2 1 . 8 8 0 3 . 2 6 8 0 3 1 . 0 2 3 2 . 5 7 4 0 4 0 . 7 2 9 2 . 2 8 2 0 5 0 . 5 7 7 2 . 1 1 5 0 6 0 ....

We have the following: Portfolio E(r) A B C Also, rf be done to eliminate the arbitrage opportunity. = .14 0.9 .16 0.8 .28 1.4 .04. Is there an arbitrage opportunity? If so, find one. Explain in...

12. What is the expected major product of this reaction sequence? NO2 1) Cl2 / FeCl3 2) H2 / Pd 3) NaNO2, HCI 4) KI A) ortho-chloroiodobenzene B) meta-chloroiodobenzene C) para-chloroiodobenzene D)...

If you were to find that two $ 4 0 0 HD televisions were missing, explain what the journal entry would be to record the theft and which financial statements would be affected.

Free cash flow valuation You are evaluating the potential purchase of a small business with no debt or preferred stock that is currently generating $ 4 2 , 7 0 0 of free cash flow ( F C F 0 = $ 4 2 ,...