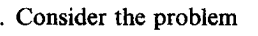
Reference Equations and Theorems

Consider the problem x + 7x2 0, (x2 -- 1)2 + (x2 5)2 = min. Draw a picture and guess the solution. Introduce a slack xz>0, and rewrite the problem in the form (1); identify A, b, C, p. Now use Theorem 2 to prove your guess is optimal: find x, u, v satisfying (13). > Look at the following problem: Ax = b, x>0 p.x+ x : Cx = minimum. = (1) Theorem 1. Suppose x solves the quadratic-programming problem (1). Then there exist vectors u in RM, v in R" such that x, u, v solve Ax = b (13) Cx + Au u V = -P x>0, v>0, X v=0. (We do not require u> 0; u is unrestricted in R.) > Theorem 2. Suppose C is positive semi-definite. Suppose x, u', v solve (13). Then x solves the quadratic program (1). If C is positive definite, then the solution of (1) is unique. Consider the problem x + 7x2 0, (x2 -- 1)2 + (x2 5)2 = min. Draw a picture and guess the solution. Introduce a slack xz>0, and rewrite the problem in the form (1); identify A, b, C, p. Now use Theorem 2 to prove your guess is optimal: find x, u, v satisfying (13). > Look at the following problem: Ax = b, x>0 p.x+ x : Cx = minimum. = (1) Theorem 1. Suppose x solves the quadratic-programming problem (1). Then there exist vectors u in RM, v in R" such that x, u, v solve Ax = b (13) Cx + Au u V = -P x>0, v>0, X v=0. (We do not require u> 0; u is unrestricted in R.) > Theorem 2. Suppose C is positive semi-definite. Suppose x, u', v solve (13). Then x solves the quadratic program (1). If C is positive definite, then the solution of (1) is unique