***SCROLL DOWN****

This is definitely a longer homework question but I have no idea how to even start answering it. I have it attached below, and I would really appreciate to whoever helps answer this if they could try to simplify it as much as possible, so I can try to follow. It's a scenario-based calculus question.

**Side note: I have done part a and now added a note of the formulas when doing the equations for part b. Thanks big time!!

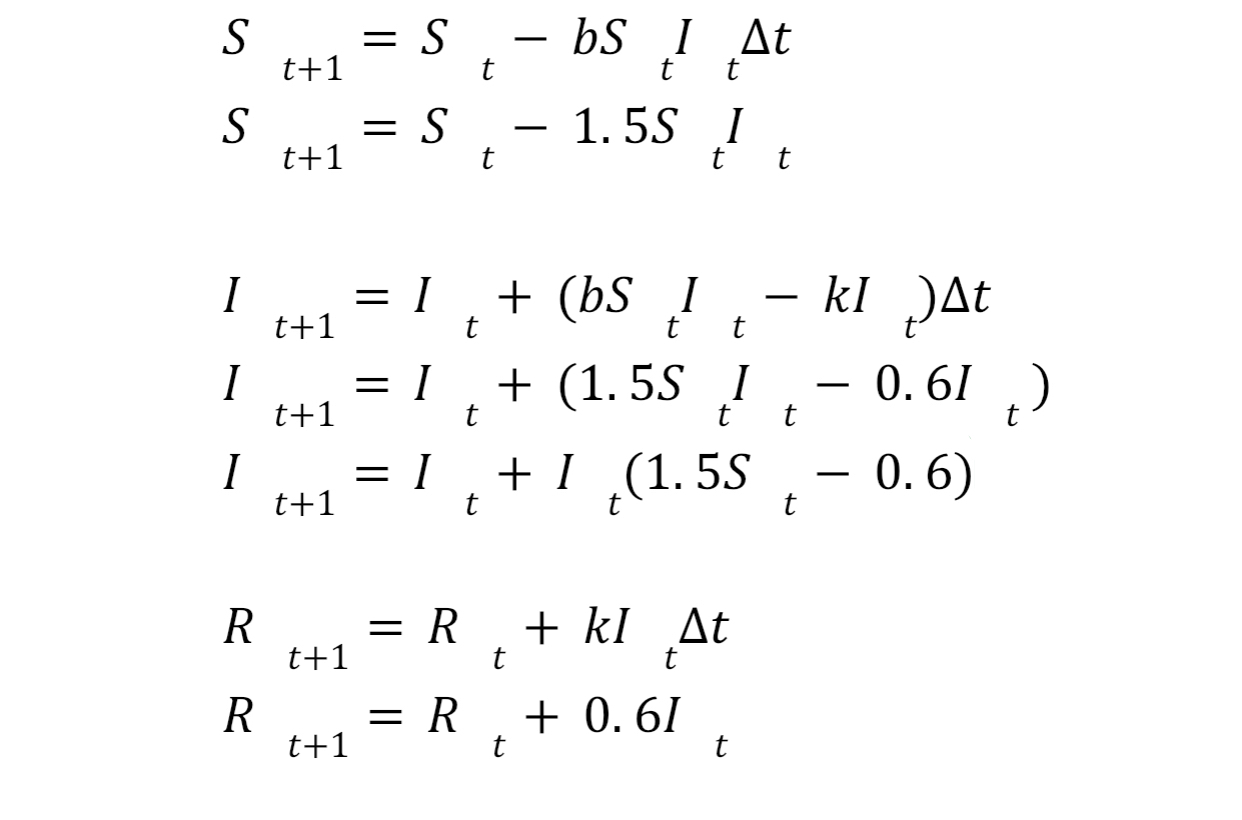
\f\fDisease spread is, of course, much more complicated than the model for infection provided earlier in this project. More accurate is the SIR model for infection, which splits a population into three distinct categories: 0 the fraction who are susceptible to a disease, represented by S (t) o the fraction who are infected with a disease, represented by I (t) O the fraction who have recovered from a disease, represented by R(t) The SIR model involved a coupled system of dilierential equations: dS E = bS(t)I(t) d! (if? E = k1\") where, as before, I: > 0 represents the rate of infection and k > 0 represents the rate of recovery. Unlike our previous model, this model assunms that once a person recovers from a disease, they cannot become sick again. We do not know how to solve these differential equations (and will not learn how to in this course), but we do know about Euler's Method to approximate solutions to a differential equation given an initial condition. The equations for using Euler's Method in the SIR model are given by S+1= S; his" I; At Ig+1= It 'i' (b8; I; kfg)At R+1= Rf, + '31; At 7. For this problem, let I: = 1.5, k = 0.6, and At = 1. Assume that time progresses by weeks, so thatt=0isweek0,t=lisweek1,andsoon. (a) Rewrite the Euler's Method formulas using the information given about b, k, and At. (Note: You do not need to show any rough work for this question.) (1)) Suppose in a population of 1000, there are 200 people infected with a disease and the rest are susceptible and no one has yet recovered, so that 300 _ 200 _ 5=m =m 0.8 In 0.2 R0 = 0 . Use a spreadsheet and Euler's Method to determine the fraction of the population suscep- tible to, infected, and recovered from this disease after 6 weeks, i.e. calculate $5, 15,.R5. Please use the exact numbers in your spreadsheet, but if lling out the table on the cover sheet you may round to three decimal places. (c) How many people in this population of 1000 are suscaptible, infected, and recovered after 6 weeks