Simulate in SIMULINK the following thermal control system

Assume that the tank is insulated to eliminate heat loss to the surrounding air. Also, that there is no heat storage in the insulation and that the liquid in the tank is perfectly mixed, so it has a stable temperature. Thus, a single temperature is used to describe that of the liquid in the tank and that of the liquid leaving. Figure 1 shows the thermal system to be simulated and the block diagram of the system.

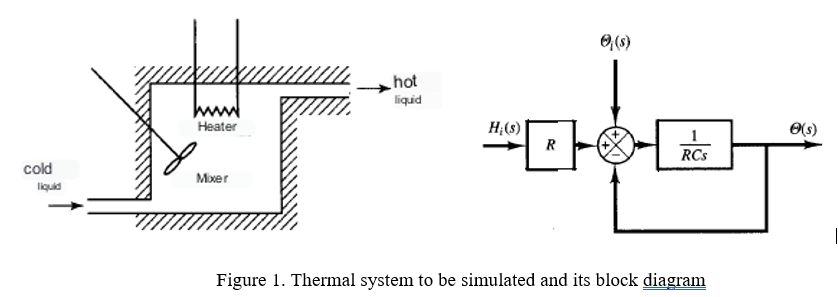
Figure 1. Thermal system to be simulated and its block diagram Where: i= steady state temperature of entering liquid, C o= steady state temperature of leaving liquid, C G= flow rate of the liquid at steady state, kg/sec M= mass of the liquid in the tank, kg c= specific heat of the liquid, kcal/kgC R= thermal resistance, Csec/kcal C= thermal capacitance, kcal/C H= steady state heat flux input, kcal/sec Suppoge we have a water storage tank and a heat source with the following characteristics: - Material: Stainless Steel - Tank height (H): 10 meters - Tank diameter (D): 2 meters - Tank surface area (A): 68.4 square meters - Tank volume (V): 31.4 cubic meters System and Controller Design We agsume that the temperature of the entering liquid remains constant and that the heat flow into the system (the heat provided by the heater) changes suddenly from a H,H+ gradually change from H to H+hi. The temperature of the leaving liquid will also change h0=Gcc=McR=h0=Gc1 The differential equation for this system is cdtd=hth0 which can be rewritten as RCdtd+=Rhi The transfer function relating to h is obtained hy Hi(s)(s)=RCs+1R In practice, the temperature of the entering liquid can fluctuate and act as a load disturbance. If it is intended to maintain a constant outlet temperature, an automatic controller can be installed that adjusts the input heat flow, jn_order.to compensate for fluctuations in the temperature of the incoming liquid. If the temperature of the entering liquid changes suddenly from i to i+i, as long as the incoming heat flux H and the liquid flow G are kept constant, the outgoing heat flux will change from HaH+h0, and the liquid temperature that comes out will change from 0 to 0+. The differential equation for this case is cdtd=Gcih0 which can be written as RCdtd+=t The transfer function that relates yi is obtained h i(s)(s)=RCs+11 If this thermal system is subject to changes in the temperature of the entering liquid and in the inflow of heat, while the flux of the liquid is kept constant, the change in the temperature of the outgoing liquid is given by the following equation. RC=8t+Rht The controller will be of the Proportional (P) type. The controller transfer function is: C(s)=Kn Once we have the model of the sygtem and the P controller designed, we can simulate the system in Simulink