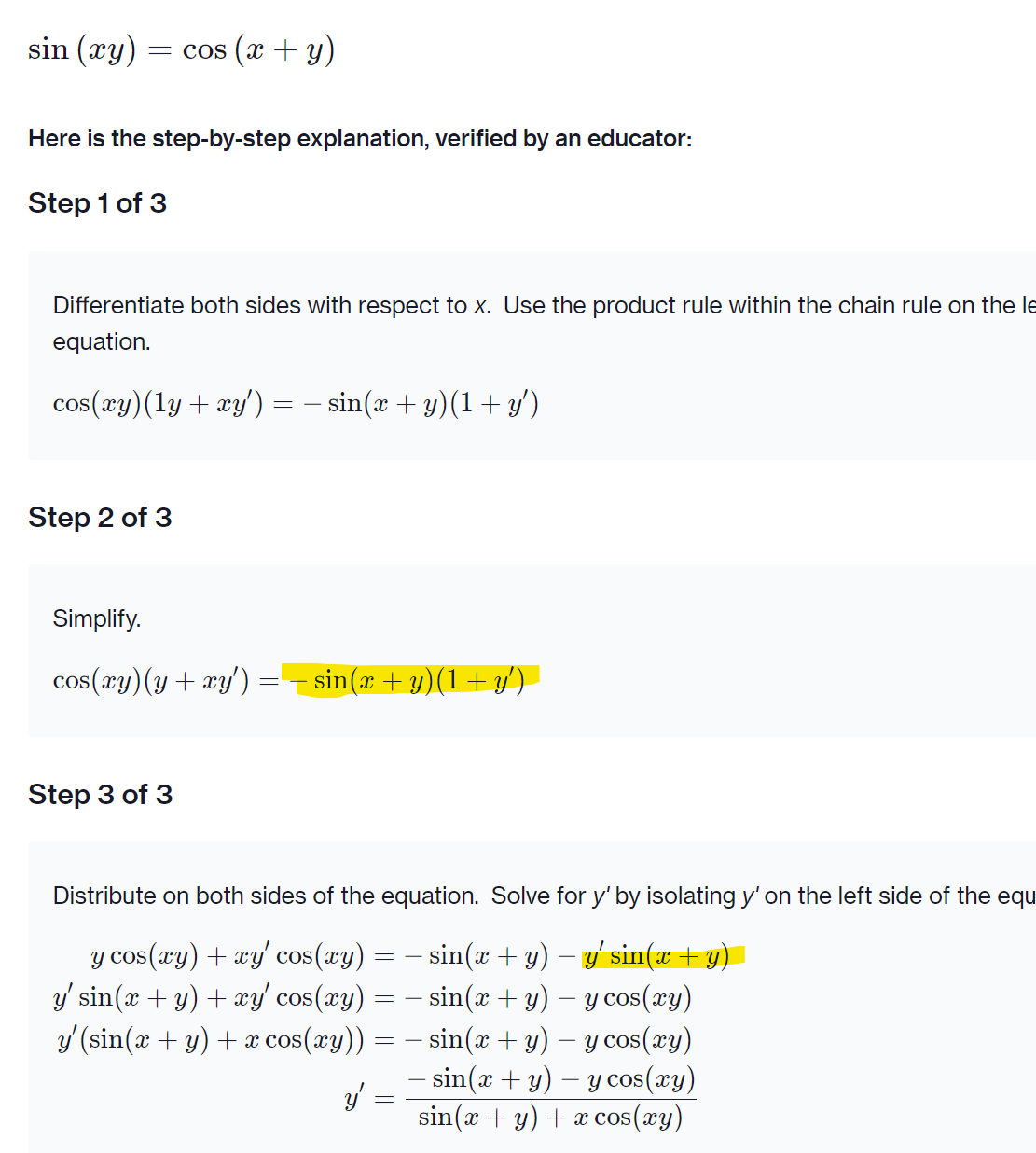
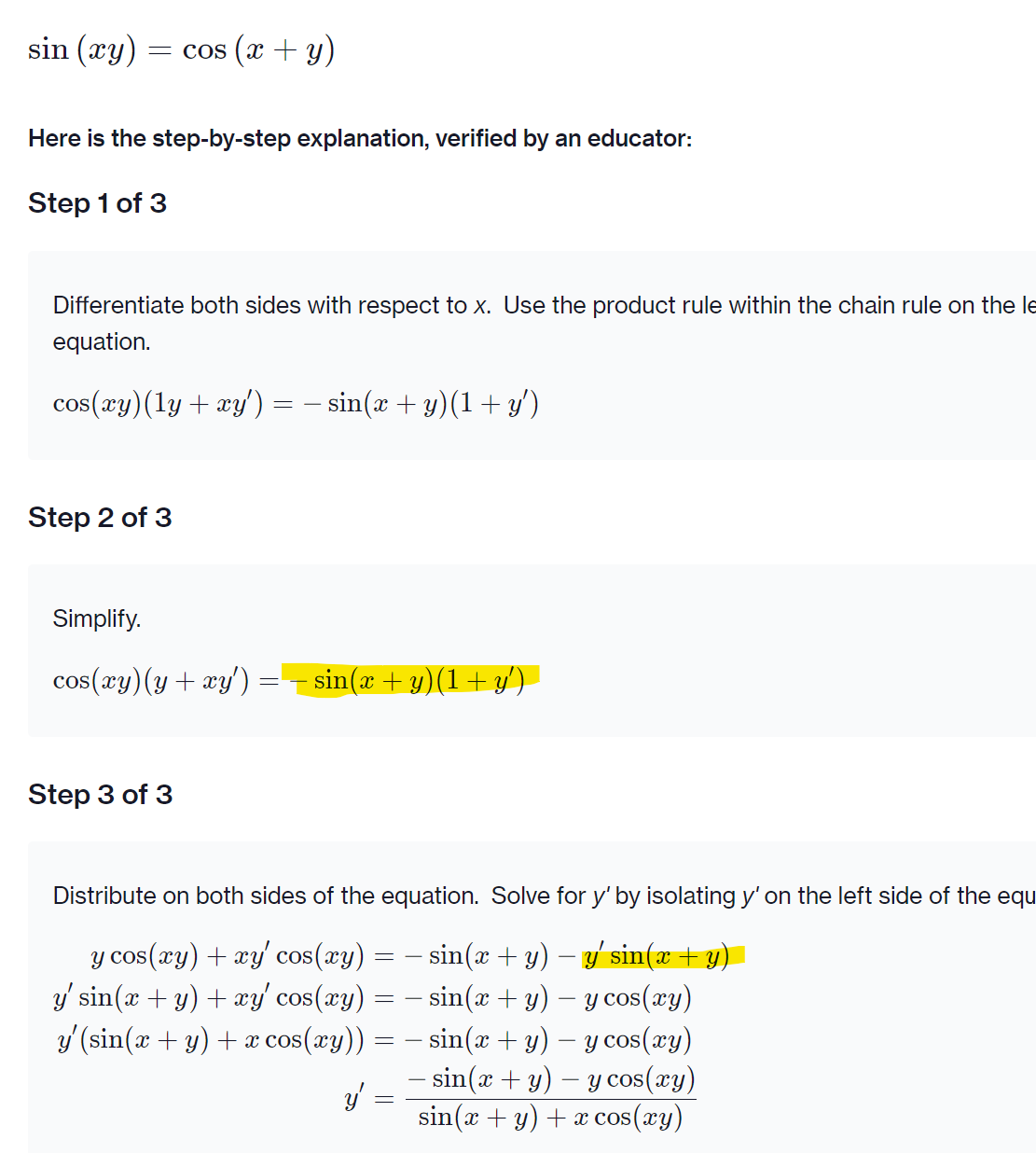
sin (xy) = cos (x + y) Here is the step-by-step explanation, verified by an educator: Step 1 of 3 Differentiate both sides with respect to x. Use the product rule within the chain rule on the l equation. cos(xy) (ly + xy' ) = - sin(x + y) (1+ y') Step 2 of 3 Simplify. cos(xy) (y + xy') = sin(x + y)(1ty) Step 3 of 3 Distribute on both sides of the equation. Solve for y' by isolating y' on the left side of the equ y cos(xy) + xy cos(xy) = - sin(x + y) - y'sin(a + y) y'sin(x + y) + xy' cos(xy) = - sin(x + y) - y cos(xy) y' (sin(x + y) + x cos(xy)) = - sin(x ty) - y cos(xy) y = - sin(x + y) - y cos(xy sin(x + y) + x cos(xy)