Solve Problem 18.32

Problems 18.1 & 18.3 Provided for Reference

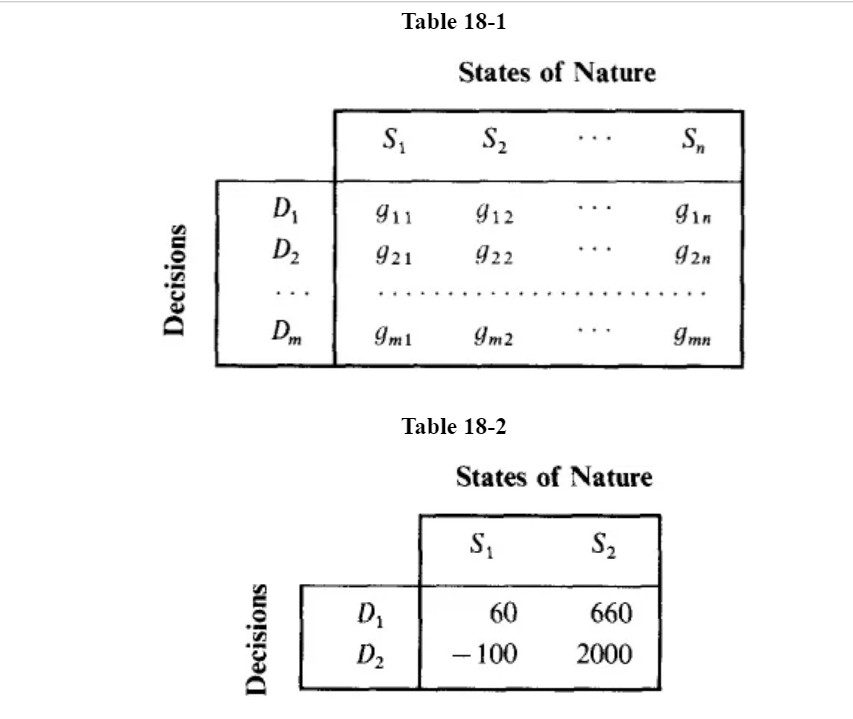
18.1 Determine recommended decisions under each naive criterion for the process described in Example 18.1. The gain matrix for this process is Table 18-2. The minimum gain for decision D is 60, while that for D2 is -100. Since max {60, 100) = 60 is the gain associated with D1, D1 is the recommended decision under the minimax criterion. The largest entry in the matrix is 2000, the gain associated with D2. Therefore D2 is the recommended decision under the optimistic criterion. The averages of the maximum and minimum gains for D, and D2 are, respectively, 660 + 60 2000 + (-100) 360 and 950 2 18.3 Determine the recommended decision under the a priori criterion for the process of Example 18.1, if the landowner estimates the probability of finding gas as 0.6. With P(S2) = 0.6 it follows that P(Si) = 1 0.6 = 0.4. Using the data in Table 18- 2, we calculate the expected gain from D, as = E(G) = (60)(0.4) + (660)(0.6) = 420 and the expected gain from D2 as E(G2) = (-100) (0.4) + (2000) (0.6) = 1160 18.32 Solve Problems 18.1 and 18.3 using the regret matrix instead of Table 18-2. Thereby verify that recommended decisions with a regret matrix need not be the same as those with a gain matrix under naive criteria, but the two matrices always yield the same recommended decision under the a priori criterion. Table 18-1 States of Nature S, S2 Si n 911 912 gin D D2 921 922 92n Decisions Dom 9m1 9m2 9mn Table 18-2 States of Nature S, S2 60 Decisions D D2 660 2000 - 100 18.1 Determine recommended decisions under each naive criterion for the process described in Example 18.1. The gain matrix for this process is Table 18-2. The minimum gain for decision D is 60, while that for D2 is -100. Since max {60, 100) = 60 is the gain associated with D1, D1 is the recommended decision under the minimax criterion. The largest entry in the matrix is 2000, the gain associated with D2. Therefore D2 is the recommended decision under the optimistic criterion. The averages of the maximum and minimum gains for D, and D2 are, respectively, 660 + 60 2000 + (-100) 360 and 950 2 18.3 Determine the recommended decision under the a priori criterion for the process of Example 18.1, if the landowner estimates the probability of finding gas as 0.6. With P(S2) = 0.6 it follows that P(Si) = 1 0.6 = 0.4. Using the data in Table 18- 2, we calculate the expected gain from D, as = E(G) = (60)(0.4) + (660)(0.6) = 420 and the expected gain from D2 as E(G2) = (-100) (0.4) + (2000) (0.6) = 1160 18.32 Solve Problems 18.1 and 18.3 using the regret matrix instead of Table 18-2. Thereby verify that recommended decisions with a regret matrix need not be the same as those with a gain matrix under naive criteria, but the two matrices always yield the same recommended decision under the a priori criterion. Table 18-1 States of Nature S, S2 Si n 911 912 gin D D2 921 922 92n Decisions Dom 9m1 9m2 9mn Table 18-2 States of Nature S, S2 60 Decisions D D2 660 2000 - 100