solve the question

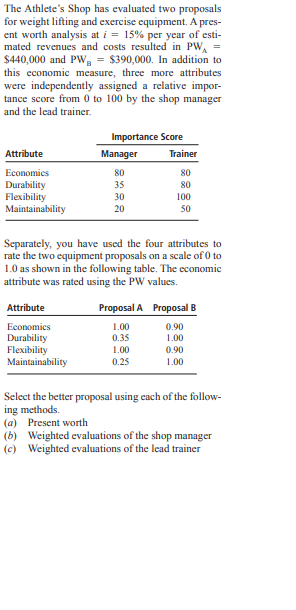
An instructor has given a short quiz consisting of two parts. For a randomly selected student, let X = the number of points earned on the first part and Y=the number of points earned on the second part. Suppose that the joint pmf of X and Y is given in the accompanying table. y p(x, y) 0 5 10 15 02 .06 .02 .10 X .04 .15 .20 .10 10 01 .15 .14 01 a. If the score recorded in the grade book is the total number of points earned on the two parts, what is the expected recorded score E(X + Y)? b. If the maximum of the two scores is recorded, what is the expected recorded score?Over the last few years, Carol's Fashion Store, a statewide franchise, has experienced the D-E mixes and costs of debt and equity capital on sev- eral projects summarized below. (a) Plot debt, equity, and weighted average cost of capital. (b) Determine what mix of debt and equity capi- tal provided the lowest WACC. Debt capital Equity capital Project Percent Rate Percent Rate A 100% 14.5% B 70 13.0 30% 7.8% C 65 12.0 35 7.8 50 11.5 7.9 35 9.9 65 9.8 20 12.4 20 125 100 12 5 For Problem 10.19, use a spreadsheet to (a) deter- mine the best D-E mix and (b) determine the best D-E mix if the cost of debt capital increases by 10% per year, for example, 13.0% increases to 14.3%A project to extend irrigation canals into an area that was recently cleared of mesquite trees (a nui- sance tree in Texas) and large weeds is projected to have a capital cost of $2,000,000. Annual mainte- nance and operation costs will be $100,000 per year. Annual favorable consequences to the gen- cral public of $820,000 per year will be offset to some extent by annual adverse consequences of $400,000 to a portion of the general public. If the project is assumed to have a 20-year life, what is the B/C ratio at an interest rate of 8% per year? Calculate the B/C ratio for the following cash flow estimates at a discount rate of 7% per year. tem Cash Flow FW of benefits, $ 30,800,000 AW of disbenefits, $ per year 105,000 First cost, $ 1,200,000 M&O costs, $ per year 400,000 Life of project, years 20 The benefits associated with a nuclear power plant cooling water filtration project located on the Ohio River are $10,000 per year forever, starting in year 1. The costs are $50,000 in year 0 and $50,000 at the end of year 2. Calculate the B/C ratio at i = 10% per year.The Athlete's Shop has evaluated two proposals for weight lifting and exercise equipment. A pres- ent worth analysis at i = 15% per year of esti- mated revenues and costs resulted in PW = $440,000 and PW = $390,000. In addition to this economic measure, three more attributes were independently assigned a relative impor- tance score from 0 to 100 by the shop manager and the lead trainer. Importance Score Attribute Manager Trainer Economics 20 80 Durability 35 80 Flexibility 30 100 Maintainability 20 50 Separately, you have used the four attributes to rate the two equipment proposals on a scale of 0 to 1.0 as shown in the following table. The economic attribute was rated using the PW values. Attribute Proposal A Proposal B Economics 1.00 0.90 Durability 0.35 1.00 Flexibility 1.00 0.90 Maintainability 0.25 1.00 Select the better proposal using each of the follow- ing methods. (a) Present worth (b) Weighted evaluations of the shop manager (c) Weighted evaluations of the lead trainerAn engineer with Haliburton calculated the AW values shown for a presently owned machine by using estimates he obtained from the vendor and company records. Retention AW Value. Period, Years $ per Year - 92,000 -81,000 -87,000 -89 000 -95,000 A challenger has an economic service life of 7 years with an AW of $-86,000 per year. Assume that used machines like the one presently owned will always be available and that the MARK is 12% per year. If all future costs remain as esti- mated for the analysis, the company should pur- chase the challenger: (a) Now (b) After 2 years (c) After 3 years (d) NeverIn a road-paving process, asphalt mix is delivered to the hopper of the paver by trucks that haul the material from the batching plant. The article "Modeling of Simultaneously Continuous and Stochastic Construction Activities for Simulation" U. of Construction Engr. and Mgmnt., 2013: 1037-1045) proposed a normal distribution with mean value 8.46 min and standard deviation .913 min for the rv X = truck haul time. a. What is the probability that haul time will be at least 10 min? Will exceed 10 min? b. What is the probability that haul time will exceed 15 min? c. What is the probability that haul time will be between 8 and 10 min? d. What value c is such that 98% of all haul times are in the interval from 8.46 - c to 8.4.6 + c? e. If four haul times are independently selected, what is the probability that at least one of them exceeds 10 min?The authors of the article "A Probabilistic Insulation Life Model for Combined Thermal-Electrical Stresses" (/EEE Trans. On Elect. Insulation, 1985: 519-522) state that "the Weibull distribution is widely used in statistical problems relating to aging of solid insulating materials subjected to aging and stress." They propose the use of the distribution as a model for time (in hours) to failure of solid insulating specimens subjected to AC voltage. The values of the parameters depend on the voltage and temperature; suppose a and $ = 200(values suggested by data in the article). a. What is the probability that a specimen's lifetime is at most 250? Less than 250? More than 300? b. What is the probability that a specimen's lifetime is between 100 and 250? c. What value is such that exactly 50% of all specimens have lifetimes exceeding that value?The article "Response of SiCf/Si3N4 Composites UnderStatic and Cyclic Loading-An Experimental and Statistical Analysis" (J. of Engr. Materials and Technology, 1997: 186-193) suggests that tensile strength (MPa) of composites under specified conditions can be modeled by a Weibull distribution with a = 9and B = 180. a. Sketch a graph of the density function. b. What is the probability that the strength of a randomly selected specimen will exceed 175? Will be between 150 and 175? c. If two randomly selected specimens are chosen and their strengths are independent of one another, what is the probability that at least one has a strength between 150 and 175? d. What strength value separates the weakest 10% of all specimens from the remaining 90%