Solve the test bellow

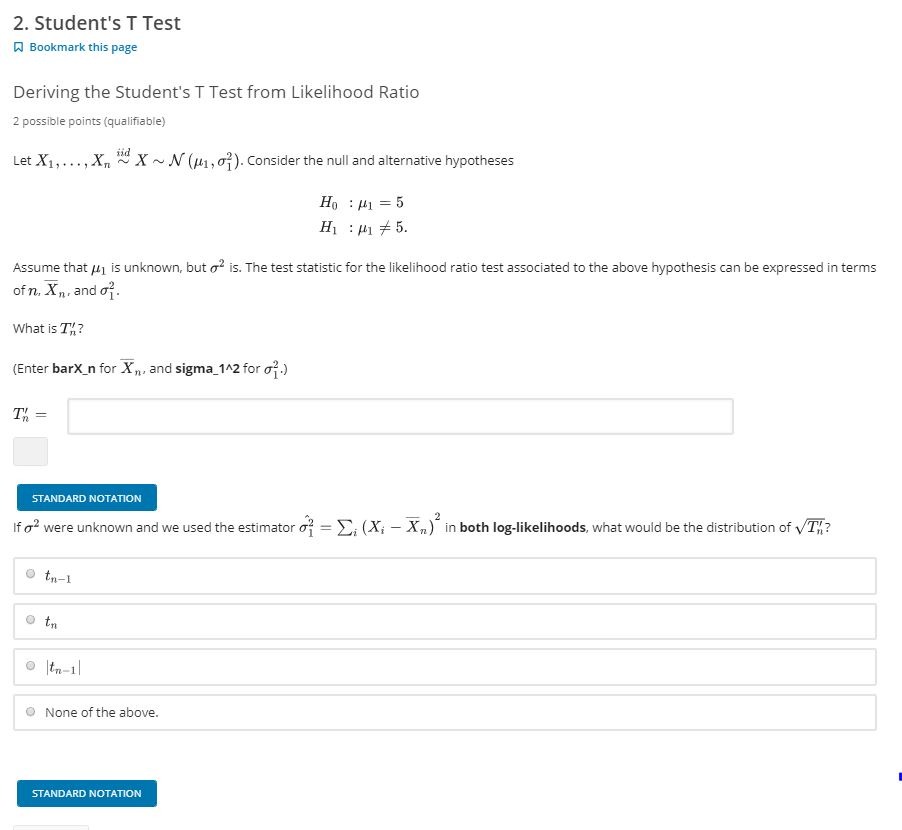
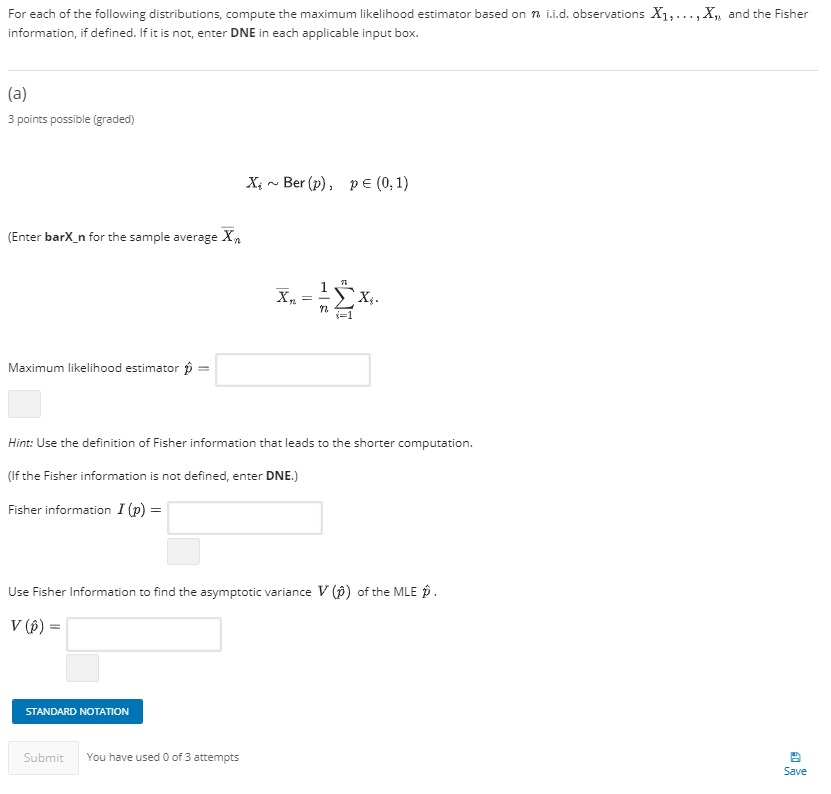
2. Student's T Test Bookmark this page Deriving the Student's T Test from Likelihood Ratio 2 possible points (qualifiable) Let X1, ..., Xn " X ~N ((1, ;). Consider the null and alternative hypotheses Ho : #1 = 5 H1 : M # 5. Assume that / is unknown, but of is. The test statistic for the likelihood ratio test associated to the above hypothesis can be expressed in terms of n. Xn . and of. What is T,? (Enter barX_n for X,, and sigma_142 for of.) T! = STANDARD NOTATION If owere unknown and we used the estimator of = _. (Xi - X. )" in both log-likelihoods, what would be the distribution of VT,? ta-1 tn O tn- 1l None of the above. STANDARD NOTATIONFor each of the following distributions, compute the maximum likelihood estimator based on n i.i.d. observations X1; ..., X, and the Fisher information, if defined. If it is not, enter DNE in each applicable input box. (a) 3 points possible (graded) Xi ~ Ber (p), DE (0, 1) (Enter barX_n for the sample average X, Xn. = = Maximum likelihood estimator p = Hint: Use the definition of Fisher information that leads to the shorter computation. (If the Fisher information is not defined, enter DNE.) Fisher information I (p) = Use Fisher Information to find the asymptotic variance V (p) of the MLE p. V (p) = STANDARD NOTATION Submit You have used 0 of 3 attempts Save