Solve this using LINGO solver, give answer in format that i can copy and paste into lingo and use the solver from there

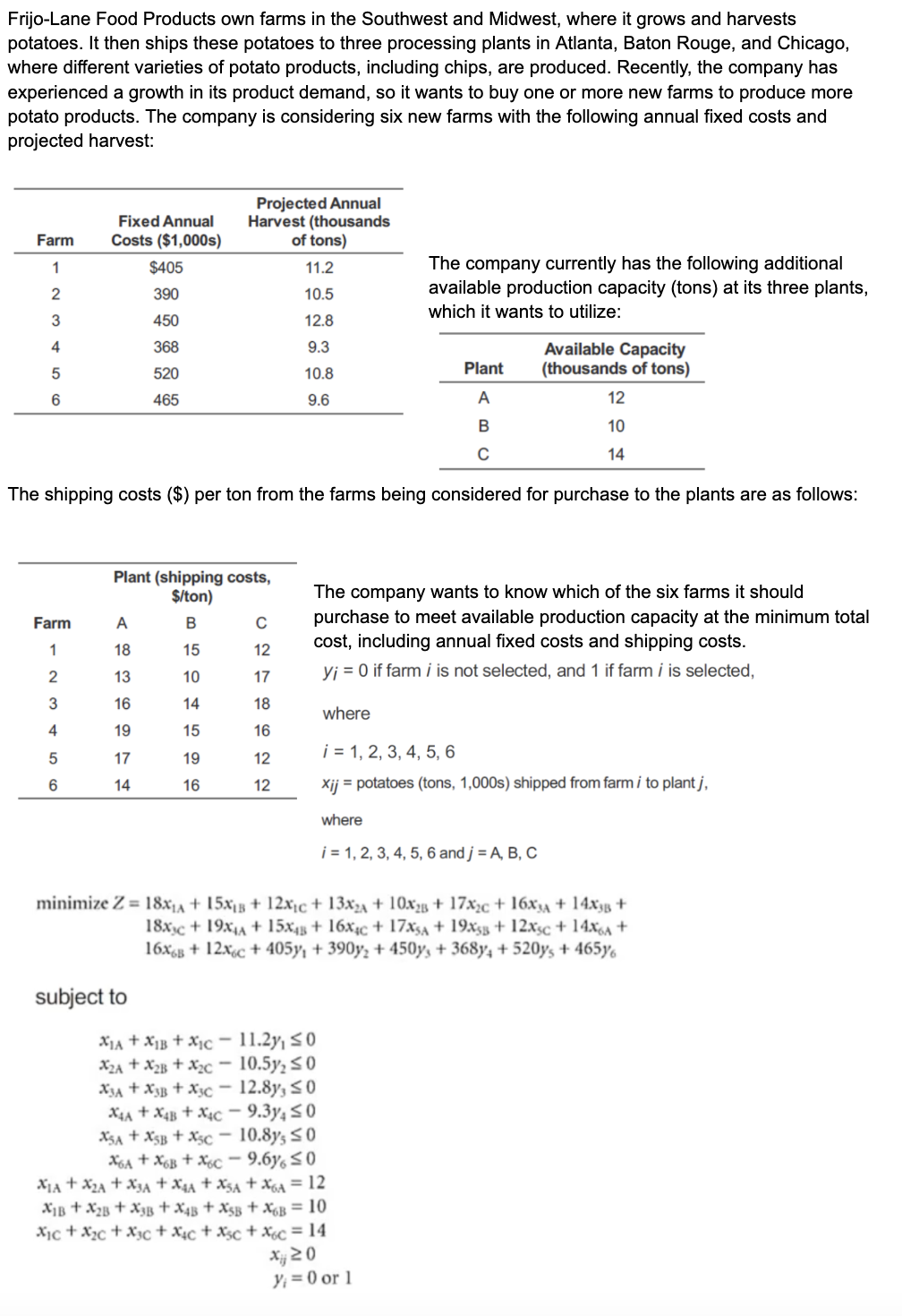
Frijo-Lane Food Products own farms in the Southwest and Midwest, where it grows and harvests potatoes. It then ships these potatoes to three processing plants in Atlanta, Baton Rouge, and Chicago, where different varieties of potato products, including chips, are produced. Recently, the company has experienced a growth in its product demand, so it wants to buy one or more new farms to produce more potato products. The company is considering six new farms with the following annual fixed costs and projected harvest: The company currently has the following additional available production capacity (tons) at its three plants, which it wants to utilize: The shipping costs \\( (\\$) \\) per ton from the farms being considered for purchase to the plants are as follows: The company wants to know which of the six farms it should purchase to meet available production capacity at the minimum total cost, including annual fixed costs and shipping costs. \\( y_{i}=0 \\) if farm \\( i \\) is not selected, and 1 if farm \\( i \\) is selected, where \\( i=1,2,3,4,5,6 \\) \\( x_{i j}= \\) potatoes (tons, 1,000 s) shipped from farm \\( i \\) to plant \\( j \\), where \\( i=1,2,3,4,5,6 \\) and \\( j=\\mathrm{A}, \\mathrm{B}, \\mathrm{C} \\) \\[ \\begin{aligned} \\operatorname{minimize} Z= & 18 x_{1 A}+15 x_{1 B}+12 x_{1 \\mathrm{C}}+13 x_{2 \\mathrm{~A}}+10 x_{2 \\mathrm{~B}}+17 x_{2 \\mathrm{C}}+16 x_{\\mathrm{AA}}+14 x_{3 \\mathrm{~B}}+ \\\\ & 18 x_{\\mathrm{BC}}+19 x_{4 \\mathrm{~A}}+15 x_{4 \\mathrm{~B}}+16 x_{4 \\mathrm{C}}+17 x_{\\mathrm{SA}}+19 x_{5 \\mathrm{~B}}+12 x_{\\mathrm{SC}}+14 x_{6 \\mathrm{~A}}+ \\\\ & 16 x_{6 \\mathrm{~B}}+12 x_{6 \\mathrm{C}}+405 y_{1}+390 y_{2}+450 y_{3}+368 y_{4}+520 y_{5}+465 y_{6} \\end{aligned} \\] subject to \\[ \\begin{aligned} x_{1 \\mathrm{~A}}+x_{1 \\mathrm{~B}}+x_{1 \\mathrm{C}}-11.2 y_{1} & \\leq 0 \\\\ x_{2 \\mathrm{~A}}+x_{2 \\mathrm{~B}}+x_{2 \\mathrm{C}}-10.5 y_{2} & \\leq 0 \\\\ x_{3 \\mathrm{~A}}+x_{3 \\mathrm{~B}}+x_{3 \\mathrm{C}}-12.8 y_{3} & \\leq 0 \\\\ x_{4 \\mathrm{~A}}+x_{4 \\mathrm{~B}}+x_{4 \\mathrm{C}}-9.3 y_{4} & \\leq 0 \\\\ x_{5 \\mathrm{~A}}+x_{5 \\mathrm{~B}}+x_{5 \\mathrm{C}}-10.8 y_{5} & \\leq 0 \\\\ x_{6 \\mathrm{~A}}+x_{6 \\mathrm{~B}}+x_{6 \\mathrm{C}}-9.6 y_{6} & \\leq 0 \\\\ x_{1 \\mathrm{~A}}+x_{2 \\mathrm{~A}}+x_{3 \\mathrm{~A}}+x_{4 \\mathrm{~A}}+x_{5 \\mathrm{~A}}+x_{6 \\mathrm{~A}} & =12 \\\\ x_{1 \\mathrm{~B}}+x_{2 \\mathrm{~B}}+x_{3 \\mathrm{~B}}+x_{4 \\mathrm{~B}}+x_{5 \\mathrm{~B}}+x_{6 \\mathrm{~B}} & =10 \\\\ x_{1 \\mathrm{C}}+x_{2 \\mathrm{C}}+x_{3 \\mathrm{C}}+x_{4 \\mathrm{C}}+x_{5 \\mathrm{C}}+x_{6 \\mathrm{C}} & =14 \\\\ x_{i j} & \\geq 0 \\\\ y_{i} & =0 \\text { or } 1 \\end{aligned} \\]