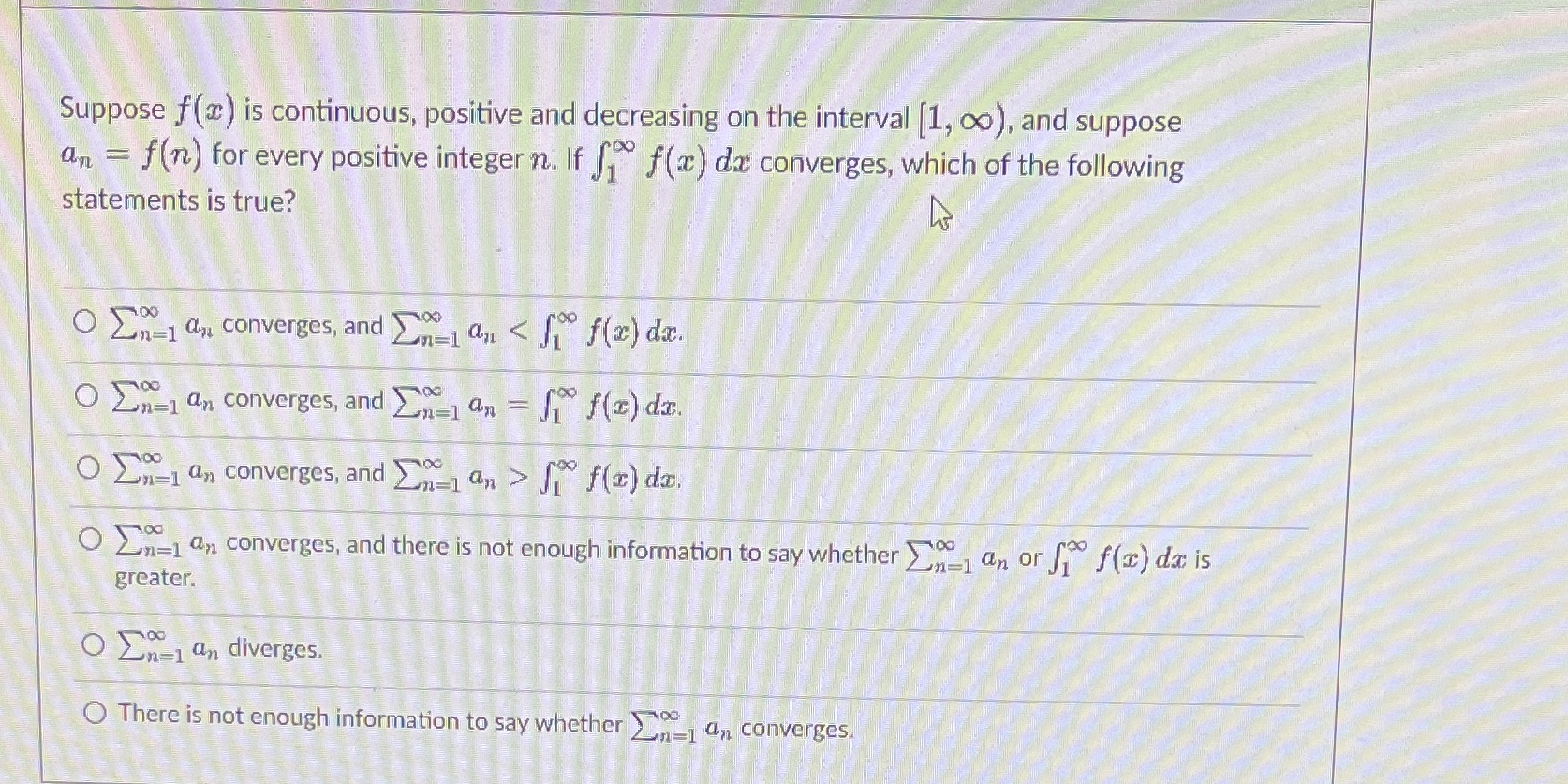
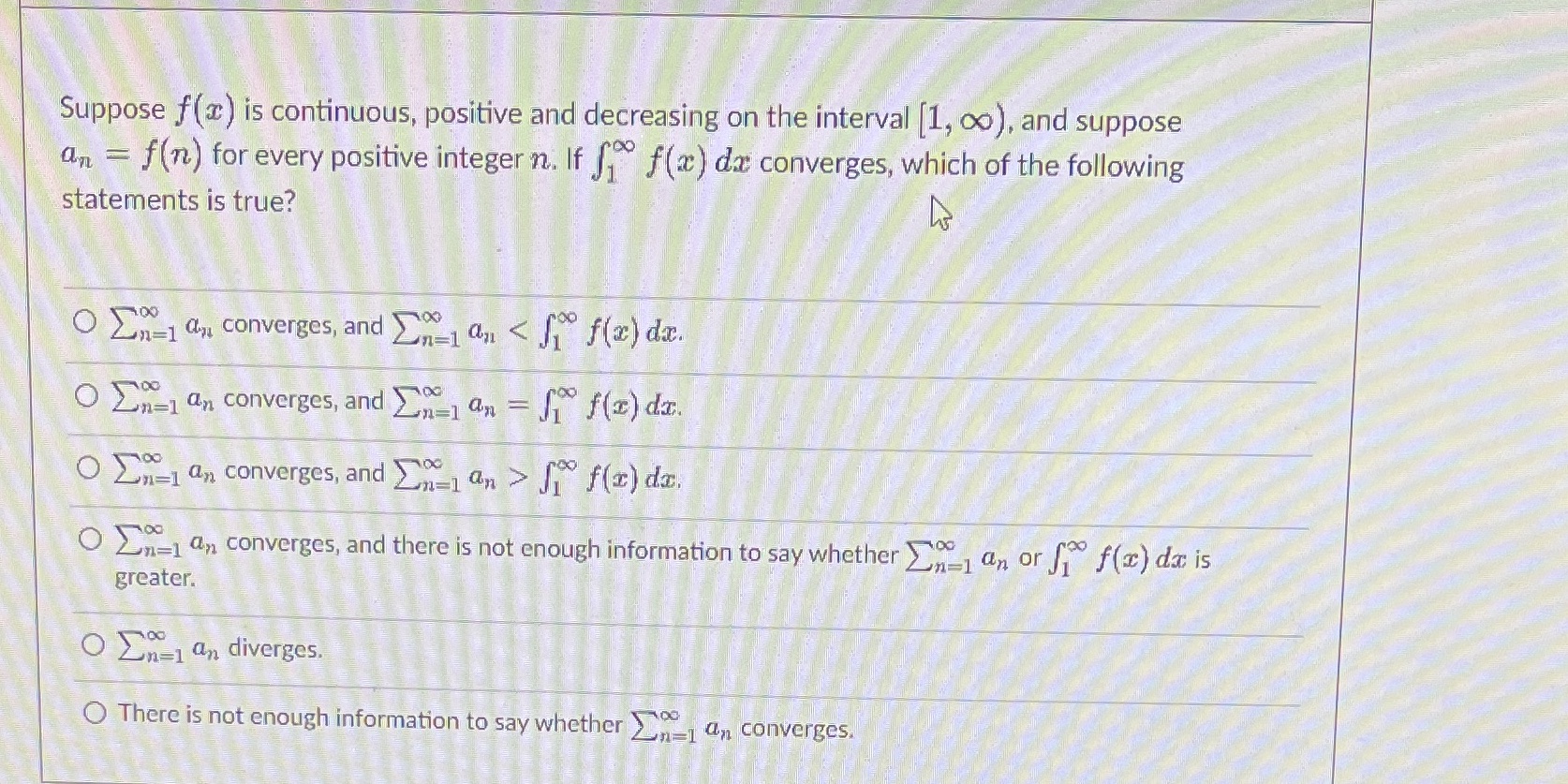
Suppose f(x) is continuous, positive and decreasing on the interval [1, co), and suppose an = f(n) for every positive integer n. If f f(x) da converges, which of the following statements is true? O En- a,, converges, and _nan ] f(x) da. O Zn=1 an converges, and there is not enough information to say whether _ an or f f(x) da is greater. O En=1 an diverges. O There is not enough information to say whether _ _ an converges