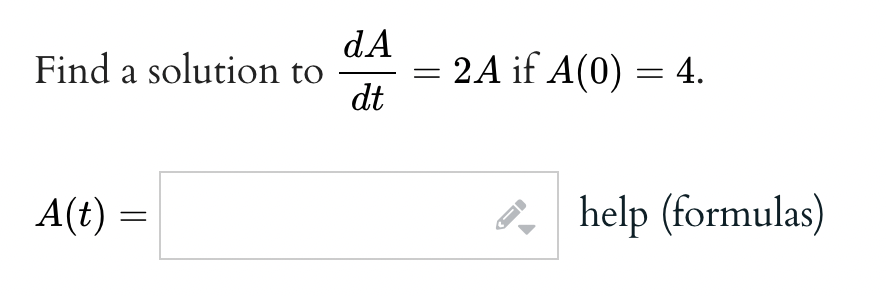
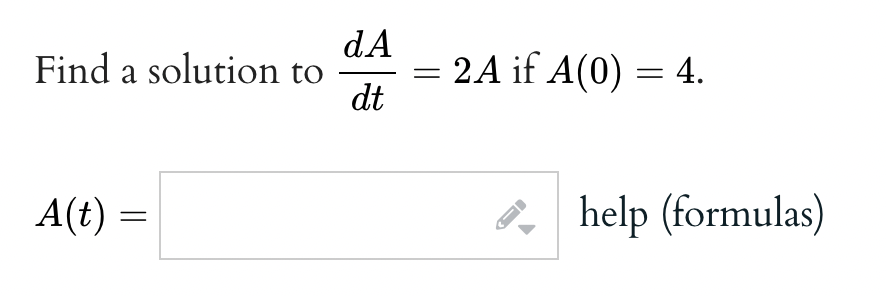
Suppose that a particle moves along an s-axis. Using ds/dt for the first derivative and d2s/dt2 for the second derivative, find differential equations whose solution is s(t) if: (a) The particle's velocity v(t) is always one-ninth of s(t). (b) The particle's acceleration a(t) is always seven times its velocity.\fThe diEerential equation I! y y = 0 has one of the following two parameter families as its general solution y = 616$ -|- 6263: 3; = cl cos(a:) + 02 sin(a:) y = cl tan(m) + 02 sec(:L') y=cl+02m Find the solution such that y(0) = 10 and y'(0) = 1: f. Let y"4y= 0. Find all values of r such that y = Ice\" satises the differential equation. If there is more than one correct answer, enter your answers as a comma separated list. 7\" = y; help (numbers) Let y' = 6x. Find all values of r such that y = rx2 satisfies the differential equation. If there is more than one correct answer, enter your answers as a comma separated list. r= help (numbers)