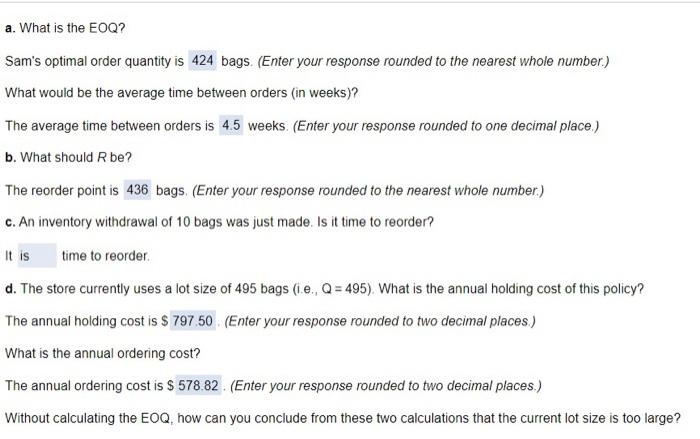
Question: The answer to letter e. is needed. Sam's Cat Hotell operates 52 weeks per year, 7 days per week, and uses a contuous review inventory
The answer to letter e. is needed.


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


