The following information is given below about a project.

$\backslash$begin$\{$tabular$\}\{|$c$|$c$|$c$|$c$|$c$|$c$|$c$|\}$

$\backslash$hline $\backslash$multirow$[$t$]\{2\}\{*\}\{$Activity$\}$ & Optimistic Time $($weeks$)$ & $\backslash$begin$\{$tabular$\}\{$l$\}$

Most $\backslash \backslash$

Likely Time $($weeks$)$

$\backslash$end$\{$tabular$\}$ & Pessimistic Time $($weeks$)$ & Expected Time $($weeks$)$ & Variance & $\backslash$multirow$[$t$]\{2\}\{*\}\{$Immediate Predecessor$($s$)\}\backslash \backslash$

$\backslash$hline & a & m & b & t & $\backslash (\backslash$sigma$^\{2\}\backslash )$ & $\backslash \backslash$

$\backslash$hline A & $4$ & $7$ & $10$ & & & $--\backslash \backslash$

$\backslash$hline B & $2$ & $8$ & $20$ & & & A $\backslash \backslash$

$\backslash$hline C & $8$ & $12$ & $16$ & & & A $\backslash \backslash$

$\backslash$hline D & $1$ & $2$ & $3$ & & & B $\backslash \backslash$

$\backslash$hline E & $6$ & $8$ & $22$ & & & D$,$ C $\backslash \backslash$

$\backslash$hline F & $2$ & $3$ & $4$ & & & C $\backslash \backslash$

$\backslash$hline G & $2$ & $2$ & $2$ & & & F $\backslash \backslash$

$\backslash$hline H & $6$ & $8$ & $10$ & & & F $\backslash \backslash$

$\backslash$hline I & $4$ & $8$ & $12$ & & & E$,$ G$,$ H $\backslash \backslash$

$\backslash$hline J & $1$ & $2$ & $3$ & & & I $\backslash \backslash$

$\backslash$hline

$\backslash$end$\{$tabular$\}$

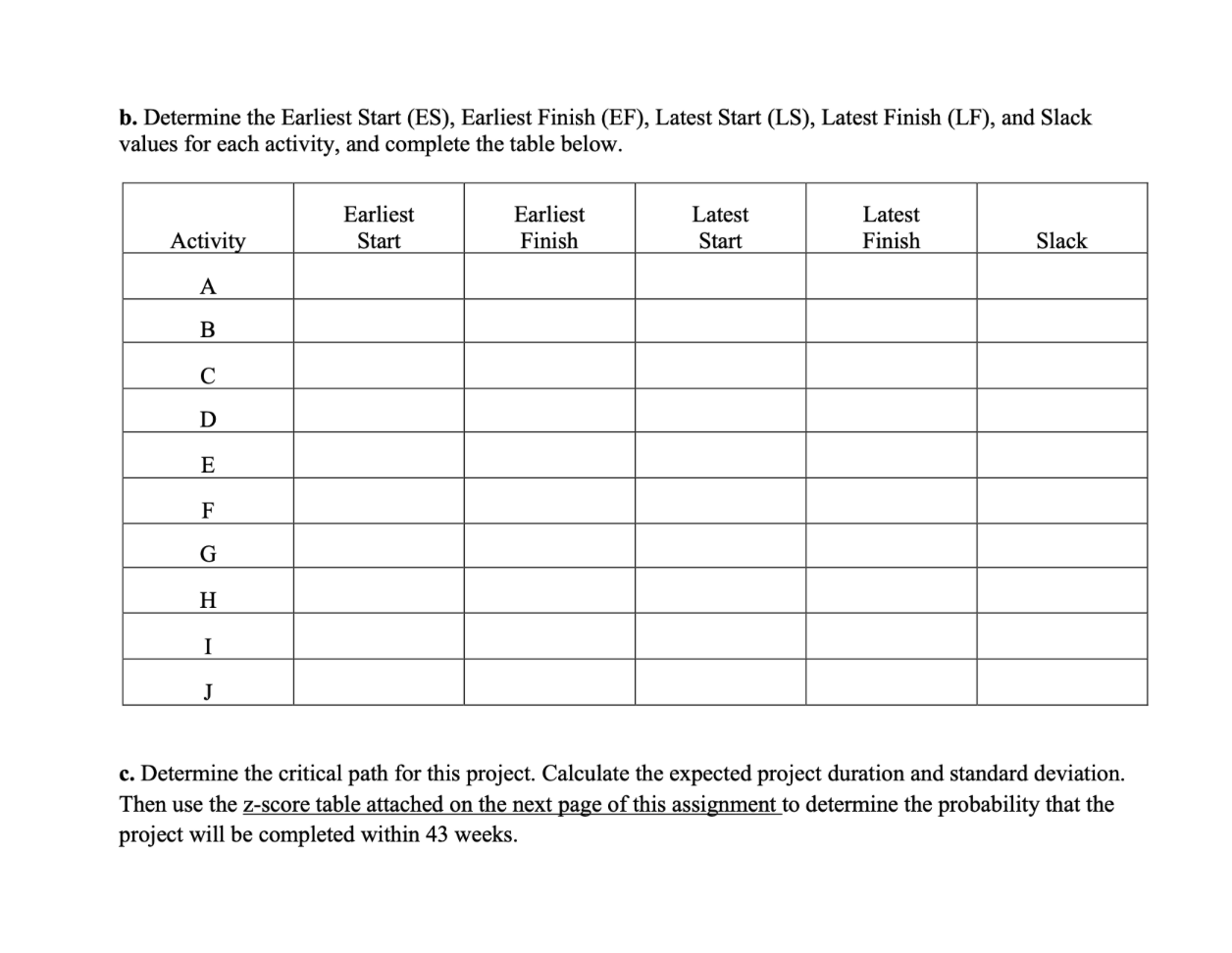
a$.$ Determine the expected activity time $\backslash (($t$)\backslash )$ and variance $\backslash (\backslash$left$(\backslash$sigma$^\{2\}\backslash$right$)\backslash )$ for each activity. Draw the network diagram using the expected times and the precedence information in the above table. b$.$ Determine the Earliest Start $($ES$),$ Earliest Finish $($EF$),$ Latest Start $($LS$),$ Latest Finish $($LF$),$ and Slack values for each activity, and complete the table below.

$\backslash$begin$\{$tabular$\}\{|$c$|$c$|$c$|$c$|$c$|$c$|\}$

$\backslash$hline Activity & $\backslash$begin$\{$tabular$\}\{$c$\}$

Earliest $\backslash \backslash$

Start

$\backslash$end$\{$tabular$\}$ & $\backslash$begin$\{$tabular$\}\{$c$\}$

Earliest $\backslash \backslash$

Finish

$\backslash$end$\{$tabular$\}$ & $\backslash$begin$\{$tabular$\}\{$c$\}$

Latest $\backslash \backslash$

Start

$\backslash$end$\{$tabular$\}$ & $\backslash$begin$\{$tabular$\}\{$c$\}$

Latest $\backslash \backslash$

Finish

$\backslash$end$\{$tabular$\}$ & Slack $\backslash \backslash$

$\backslash$hline A & & & & & $\backslash \backslash$

$\backslash$hline B & & & & & $\backslash \backslash$

$\backslash$hline C & & & & & $\backslash \backslash$

$\backslash$hline D & & & & & $\backslash \backslash$

$\backslash$hline E & & & & & $\backslash \backslash$

$\backslash$hline F & & & & & $\backslash \backslash$

$\backslash$hline G & & & & & $\backslash \backslash$

$\backslash$hline H & & & & & $\backslash \backslash$

$\backslash$hline I & & & & & $\backslash \backslash$

$\backslash$hline J & & & & & $\backslash \backslash$

$\backslash$hline

$\backslash$end$\{$tabular$\}$

c$.$ Determine the critical path for this project. Calculate the expected project duration and standard deviation. Then use the z$-$score table attached on the next page of this assignment to determine the probability that the project will be completed within $43$ weeks. The following information is given below about a project.

$\backslash$begin$\{$tabular$\}\{|$c$|$c$|$c$|$c$|$c$|$c$|$c$|\}$

$\backslash$hline $\backslash$multirow$[$t$]\{2\}\{*\}\{$Activity$\}$ & Optimistic Time $($weeks$)$ & $\backslash$begin$\{$tabular$\}\{$l$\}$

Most $\backslash \backslash$

Likely Time $($weeks$)$

$\backslash$end$\{$tabular$\}$ & Pessimistic Time $($weeks$)$ & Expected Time $($weeks$)$ & Variance & $\backslash$multirow$[$t$]\{2\}\{*\}\{$Immediate Predecessor$($s$)\}\backslash \backslash$

$\backslash$hline & a & m & b & t & $\backslash (\backslash$sigma$^\{2\}\backslash )$ & $\backslash \backslash$

$\backslash$hline A & $4$ & $7$ & $10$ & & & $--\backslash \backslash$

$\backslash$hline B & $2$ & $8$ & $20$ & & & A $\backslash \backslash$

$\backslash$hline C & $8$ & $12$ & $16$ & & & A $\backslash \backslash$

$\backslash$hline D & $1$ & $2$ & $3$ & & & B $\backslash \backslash$

$\backslash$hline E & $6$ & $8$ & $22$ & & & D$,$ C $\backslash \backslash$

$\backslash$hline F & $2$ & $3$ & $4$ & & & C $\backslash \backslash$

$\backslash$hline G & $2$ & $2$ & $2$ & & & F $\backslash \backslash$

$\backslash$hline H & $6$ & $8$ & $10$ & & & F $\backslash \backslash$

$\backslash$hline I & $4$ & $8$ & $12$ & & & E$,$ G$,$ H $\backslash \backslash$

$\backslash$hline J & $1$ & $2$ & $3$ & & & I $\backslash \backslash$

$\backslash$hline

$\backslash$end$\{$tabular$\}$

a$.$ Determine the expected activity time $\backslash (($t$)\backslash )$ and variance $\backslash (\backslash$left$(\backslash$sigma$^\{2\}\backslash$right$)\backslash )$ for each activity. Draw the network diagram using the expected times and the precedence information in the above table.